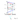РАЗДЕЛ II. ПЕРСПЕКТИВА

Наглядность изображения – одна из главных задач архитектурного чертежа. Изображения фасадов с построенными на них тенями не всегда позволяют понять и представить себе композиционное решение. С этой целью строятся перспективные изображения зданий, комплекса зданий. Оценить решение интерьера также невозможно без построения его перспективы. Поэтому умение грамотно построить перспективное изображение один из необходимых навыков для архитекторов и дизайнеров.
В зависимости от того, на какой поверхности строится перспективное изображение, перспектива подразделяется на следующие виды:
– линейная перспектива – перспективное изображение, построенное на плоскости;
– панорамная или цилиндрическая перспектива – перспективное изображение, построенное на внутренней поверхности цилиндра вращения;
– купольная или сферическая перспектива – перспективное изображение, построенное на внутренней поверхности сферы.
В настоящем курсе рассматривается только линейная перспектива.

Метод центрального проецирования является основным средством построения перспективных изображений. На рис.1.1 представлены плоскости проекций П₁ и П₂, а также дополнительная плоскость K, называемая картинной плоскостью или просто картиной, расположенная перпендикулярно горизонтальной плоскости проекций Π₁. В данном примере для упрощения построений картинная плоскость располагается параллельно фронтальной плоскости проекций, что не является обязательным. Линия пересечения картины k с горизонтальной плоскостью проекций называется основанием картины. Точка A расположена в пространстве между плоскостями Π₂ и K. Это пространство называется предметным. Наблюдатель находится в пространстве перед плоскостью K. Это пространство называется промежуточным пространством. Пространство за наблюдателем называется мнимым пространством. Точка S₁ на горизонтальной плоскости проекций, в которой стоит наблюдатель, называется точкой стояния. Точка S, находящаяся в промежуточном пространстве и на уровне которой расположены глаза наблюдателя, называется точкой зрения. Луч SP, проведенный из точки зрения перпендикулярно картинной плоскости, называется главным лучом. Точка его пересечения с картинной плоскостью P называется главной точкой картины. Линия h, проходящая через главную точку P параллельно основанию картины, называется линией горизонта.
Точки A₁ и A₂ являются горизонтальной и фронтальной проекциями точки A на плоскости проекций Π₁ и Π₂. При пересечении с основанием картины луча, проведенного из точки S₁ в точку A₁, образуется точка A₀. Точка A₀ называется основанием точки A. Пересечение луча, исходящего из точки S в точку A, с вертикальной линией из точки A₀ образуется точка A^/. Точка A^/ называется перспективной проекцией точки A на плоскость K (точки S, S₁, A₀, A₁, A, A^/ лежат в одной вертикальной плоскости). Одна проекция A^/ не дает обратимого чертежа точки A, т.к. для любой точки, принадлежащей лучу SA, перспективная проекция совпадет с точкой A^/. Для того, чтобы чертеж обладал обратимостью, строится вторичная перспективная проекция точки A, полученная в пересечении луча SA₁ с картинной плоскостью в точке A^/₁. Точка A^/₁ называется вторичной перспективной проекцией точки A. Комплекс точек A^/ и A^/₁ однозначно определяет положение точки A.

Для построения перспективы отрезка AB (рис.1.2) необходимо для точки B провести построения как для точки A. Перспектива отрезка прямой для линейной перспективы также является отрезком прямой. Поэтому, соединив точки A^/ и B^/, а также точки A^/₁ и B^/₁ прямой линией, можно получить перспективную проекцию A^/B^/ и вторичную проекцию A^/₁B^/₁ отрезка AB.

На рис.1.3 изображен комплексный чертеж отрезка AB, а также картинная плоскость K, которая по отношению к комплексному чертежу является фронтальной плоскостью уровня. Фронтальная проекция плоскости K совпадает с фронтальной плоскостью проекций Π₂. На этом чертеже показано, как, имея комплексный чертеж, можно построить перспективное изображение. Однако, на практике перспективное изображение строится другим более простым способом. Возвращаясь к изображению на рис.1.2, перспективную проекцию отрезка AB можно построить через полную перспективу прямой, на которой лежит отрезок AB. Для этого необходимо продолжить прямую по обе стороны от точек A и B. Прямая при ее продолжении за точку A пересечет картинную плоскость в точке N. Очевидно, что перспектива точки N, лежащей в картинной плоскости, совпадет с этой точкой N^/≡N, а ее вторичная перспективная проекция совпадет с основанием точки N^/ (N^/₁≡N₀). На рис.1.4 для получения точек N^/ и N^/₁ достаточно продолжить горизонтальную проекцию A₁B₁ до пересечения с горизонтальной проекцией картинной плоскости K, а на фронтальной проекции картинной плоскости продолжить фронтальную проекцию A₂B₂ до пересечения с соответствующей линией связи.
Если продолжить отрезок за точку B, то точки прямой будут удаляться от картинной плоскости (рис.1.2). При этом луч, исходящий из точки S, в пределе займет положение, параллельное отрезку AB (соответственно проекции луча займут положение, параллельное соответствующим проекциям, на рис.1.2, 1.4 и далее одинаковыми штрихами обозначены параллельные прямые). В точке F^/ будет находиться, так называемый, конец прямой, а отрезок N^/F^/ будет называться полной перспективой прямой, на которой лежит отрезок AB. В точке F^/₁ будет находиться конец вторичной перспективной проекции прямой. Отрезок N^/₁F^/₁ будет называться полной вторичной перспективной проекцией прямой, на которой лежит отрезок AB. Точка F^/ называется точкой схода прямой, точка F^/₁ называется точкой схода вторичной перспективной проекции. Точка F₀ называется основанием точки схода. Точка схода вторичной перспективной проекции F^/₁ всегда находится на линии горизонта h. Аналогичные построения выполнены на рис.1.4 при совмещении картинной плоскости с комплексным чертежом.

Таким образом, для построения перспективы отрезка необходимо иметь комплексный чертеж, на котором строится начало прямой N и точка схода F^/. Далее отдельно строится картина (рис.1.5), на которой вдоль ее основания откладываются точки N^/₁≡N₀ и F₀. Все горизонтальные расстояния берутся с горизонтальной проекции комплексного чертежа (обычно они откладываются на основании картины от основания главной точки P₀). От точек N₀ и F₀ по вертикали откладываются расстояния, равные высотам точек N^/ и F^/, которые берутся с фронтальной проекции комплексного чертежа (т.к. точки N^/ и F^/ находятся в картинной плоскости, то их высоты будут на картине в натуральную величину). Соединяя точки N^/ и F^/, а также N^/₁ и F^/₁, можно получить полную перспективу прямой и ее вторичной проекции. Если на основании картины от точки P₀ отложить расстояния до точек A₀ и B₀ (взятые с горизонтальной проекции комплексного чертежа) и провести через них вертикальные прямые, то они отсекут на полной перспективе и ее вторичной проекции соответствующие перспективную проекцию отрезка A^/B^/ и его вторичную перспективную проекцию A^/₁B^/₁.
Очевидно, что параллельные прямые будут иметь общую точку схода (рис.1.6).

При построении перспективы реальных архитектурных форм чаще всего приходится строить перспективные проекции прямых частного положения или имеющих какие-либо особые свойства. Поэтому учет особенностей при построении перспективы таких прямых дает дополнительные возможности для упрощения построений.

Точка схода горизонтальных прямых находится на линии горизонта (рис.2.1). Действительно, прямая, исходящая из точки зрения и параллельная горизонтальной прямой, также будет горизонтальной, и поэтому точка схода F^/ будет находиться на линии горизонта, т.е. точки F^/₁ и F^/ совпадут.

Точка схода прямых, перпендикулярных картине, совпадает с главной точкой картины, т.к. луч, исходящий из точки зрения и параллельный таким прямым, пересекает картинную плоскость в точке P. На рис.2.2 построена перспектива отрезка AB.

Точками схода горизонтальных прямых, расположенных под углом 45° к картинной плоскости, являются дистанционные точки (рис.2.3). Дистанционными точками называются точки D¹ и D², расположенные на линии горизонта на расстоянии от главной точки P, равном расстоянию от точки зрения до картинной плоскости SP (т.е. PD¹ = PD² = SP). Прямые, исходящие из точки S и параллельные прямым AB и BC, также расположены под углом 45° к картине и пересекают ее в точках D¹ и D².

Перспективная проекция прямой, параллельной картинной плоскости, параллельна самой прямой (рис.2.4). Т.к. такая прямая не имеет ни начала, ни точки схода, то ее перспективная проекция строится через перспективу прямых a и b, перпендикулярных картинной плоскости и проходящих через точки A и B. Вертикальные прямые из точек A₀ и B₀ пересекутся с перспективной проекцией a^/ и b^/, а также с вторичной перспективной проекцией a^/₁ и b^/₁ в точках A^/, B^/ и A^/₁, B^/₁ соответственно.
Плоские фигуры, параллельные картине, в перспективе являются подобными фигурами.

Зачастую на перспективе возникает необходимость определить натуральную величину отрезка или отложить отрезок определенной величины. Эти задачи можно решить непосредственно на перспективе, если найдется возможность каким-либо образом в картинной плоскости построить отрезок, равный заданному отрезку (т.к. отрезки, расположенные в картинной плоскости, не искажаются и проецируются в натуральную величину).

1. Определение натуральной величины отрезков, параллельных картинной плоскости (рис.3.1).
Прямая AB может быть вынесена в картинную плоскость с помощью прямых, перпендикулярных картине, имеющих точку схода главную точку P. По горизонтальной проекции видно, что прямые a и b как бы выносят отрезок AB в картинную плоскость (с этой целью можно было использовать любые параллельные прямые, но тогда необходимо было бы построить их точку схода). Точка P в этом случае называется точкой измерения, т.е. с ее помощью можно измерить натуральную величину отрезка AB.

2. Определение натуральной величины отрезков, расположенных в предметной плоскости и перпендикулярных картинной плоскости (рис.3.2).
На чертеже изображен отрезок AB. Если через конец отрезка B на горизонтальной плоскости проекций провести прямую под углом 45° к картине, то эта прямая отсечет на основании картины отрезок a, равный по величине заданному. Точкой схода для такой прямой является дистанционная точка. Поэтому если непосредственно на перспективе провести прямую через конец отрезка в дистанционную точку D¹, то она на основании картины отсечет отрезок, равный по величине отрезку AB. В данном случае точкой измерения является дистанционная точка D¹.

3. Определение натуральной величины произвольного отрезка, расположенного в предметной плоскости (рис.3.3).
Определяется точка схода F^/ заданного отрезка AB. Затем определяется точка S^h₀ вращением точки S₁ вокруг точки F₀ на горизонтальной плоскости проекций до совмещения с картиной. Из точек A₁ и B₁ проводятся прямые, параллельные S₁S^h₀. Полученный треугольник S₁S^h₀F₀ является по построению равнобедренным, а треугольник B^cB₁N₀ ему подобным, и как следствие, равнобедренным. Прямые a и b отсекают на основании картины отрезок A^cB^c, равный заданному. Точка S^h является точкой схода для отрезков a и b. На самой перспективе точка S^h определяется вращением совмещенной точки зрения S^c вокруг точки схода F^/ до линии горизонта (т.е. на картине строится треугольник S^cS^hF^/, являющийся зеркальным отражением треугольника S₁S^h₀F₀). Точка S^h является точкой измерения для любой прямой, расположенной в предметной плоскости и параллельной заданному отрезку AB.

4. Определение натуральной величины произвольного отрезка (рис.3.4).
Для определения натуральной величины произвольного отрезка необходимо знать его вторичную проекцию. Тогда, построив натуральную величину его вторичной проекции и используя ту же точку измерения S^h, можно построить натуральную величину отрезка AB.

Иногда возникает необходимость построить по известным из комплексного чертежа координатам точки ее перспективную проекцию. На комплексном чертеже координатная ось X совмещена с основанием картины, ось Z направлена перпендикулярно горизонтальной (предметной) плоскости, а Y ось направлена перпендикулярно картинной плоскости. Тогда на перспективе ось X совпадает с основанием картины, ось Z направлена вертикально, а ось Y (как прямая, перпендикулярная картине) направлена в главную точку картины P. Для построения точки A^/, имеющей координаты A(3,4,7) (рис.3.5), необходимо по оси X отложить 3 единицы, по оси Z – 7 единиц и построить прямые из точек A^/x и A^/z в главную точку P. Далее по оси X отложить 4 единицы и полученную точку соединить с дистанционной точкой D¹. Проведенная прямая отсечет на оси Y 4 единицы. Дальнейшие построения ясны из чертежа и позволяют построить точку A^/.

Прямые, перпендикулярные картине, находящиеся в координатных плоскостях и проходящие через точки деления на координатных осях X и Z, имеют точку схода в главной точке P (рис.3.6), а также прямые, параллельные картине и проходящие через точки деления оси Y, образуют перспективный масштаб. С помощью перспективного масштаба можно построить перспективу объекта по координатам отдельных точек. Кроме того, перспективный масштаб позволяет построить перспективу по клеткам, т.е. может быть использован в роли пространственной палетки.

1. Деление горизонтального отрезка пополам (рис. 3.7)
Для того, чтобы разделить отрезок AB в перспективе пополам, необходимо достроить прямоугольник ABCE, у которого сторонаCE лежит на линии горизонта, а стороны AE и BC – вертикальные. Вертикальная прямая OK, проведённая из точки пересечения диагоналей, разделит отрезок AB на две равные части.

2. Построение отрезка, равного заданному и лежащему на его продолжении (рис.3.8)
В прямоугольнике ABCE из предыдущей задачи прямая, проведённая из точки пересечения диагоналей в точку схода F^|, разделит сторону BC пополам в точке M. Прямая, проведённая из точки B через точку M до пересечения с продолжением отрезка AB в точке L, отсечет отрезок BL, равный заданному.

3. Деление горизонтального отрезка на пропорциональные части (рис.3.9).
Через ближайшую точку отрезка AB проводится горизонтальный отрезок прямой 1-5, разделённый в заданном отношении. Из последней точки 5 через конечную точку B заданного отрезка проводится прямая и продолжается до пересечения с линией горизонта в точке O. Прямые, проведённые из точки O в точки 2, 3, 4, разделят отрезок AB в перспективе в том же пропорциональном отношении, что и отрезок 1-5.

4. Деление произвольного отрезка на пропорциональные части (рис.3.10).
В случае отрезка общего положения необходимо разделить в пропорциональном отношении его вторичную проекцию, как в предыдущей задаче. Вертикальный прямые из точек деления разделят заданный отрезок в том же пропорциональном отношении.

В случае, если необходимо провести горизонтальную прямую через заданную точку C^/ параллельно заданной прямой a^/ при отсутствии точки схода в пределах чертежа (рис.3.11), необходимо через какую-нибудь точку на заданной прямой (например, A^/) провести вертикальную прямую до пересечения с линией горизонта, провести прямую, соединяющую точки A^/ и C^/, а также прямую, соединяющую точку C^/ и точку пересечения 1^/. Затем, несколько отступя, построить треугольник 2^/ – 3^/ – 4^/, стороны которого параллельны сторонам треугольника A^/C^/1^/. Прямая b^/, проведенная через точки C^/ и 4^/, будет параллельна прямой a^/.

В случае если необходимо провести не одну, а несколько прямых, параллельных заданной горизонтальной прямой a^/, вышеприведенное построение становится достаточно трудоемким. Поэтому проводится следующее построение (рис.3.12). Точки, через которые необходимо провести параллельные прямые, соединяются вертикальной прямой b^/. Несколько отступя, проводится другая вертикальная прямая c^/ . Через точку пересечения прямых c^/ и a^/ C^/ под произвольным углом проводится прямая с нанесенными делениями таким образом, чтобы точка A^/ совместилась с точкой C^/. Из точки B^/ проводится прямая, соединяющая ее с аналогичной точкой на линии горизонта, а из остальных точек деления проводятся прямые ей параллельные. Через полученные точки на вертикальной прямой c^/ и соответствующие им точки на прямой b^/ проводятся прямые, которые будут параллельны.

Построение окружности в перспективе выполняется непосредственно на картине. Для этого необходимо знать положение центра окружности, ее радиус, а также положение плоскости, в которой она расположена. Чаще всего окружность располагается в горизонтальной или вертикальной плоскостях. Расположение окружности в наклонной плоскости встречается значительно реже и в данном курсе не рассматривается. Перспективная проекция окружности может представлять собой эллипс, параболу, гиперболу, окружность, прямую. Окружность проецируется в перспективе в виде отрезка горизонтальной прямой, если она находится в горизонтальной плоскости, проходящей через линию горизонта. Окружность проецируется в виде окружности меньшего радиуса, если она находится в вертикальной плоскости, параллельной картине. Горизонтальная окружность проецируется в виде эллипса, если ее центр находится перед точкой зрения. Горизонтальная окружность проецируется в виде параболы, если ее центр совпадает с точкой зрения. Горизонтальная окружность проецируется в виде гиперболы, если ее центр находится за точкой зрения.
Как и при построении теней от окружности на комплексном чертеже, в перспективе окружность строится с помощью квадрата, описанного вокруг нее, по восьми точкам (четыре точки касания с квадратом и еще четыре точки, расположенные на диагоналях квадрата и отсекаемые на них прямыми, параллельными сторонам на расстоянии 0,707 от середины стороны квадрата).
Ниже описывается построение перспективы окружностей, расположенных в горизонтальных и вертикальных плоскостях.

Окружность вписывается в квадрат ABCE, две стороны которого AE и BC параллельны картинной плоскости (рис.4.1). Тогда две другие стороны AB и CE перпендикулярны картинной плоскости и их точка схода, а также прямых им параллельных, находится в главной точке P. Через заданный центр окружности O^/ проводится прямая в точку схода P и доводится до основания картины. Эта прямая является полной перспективой прямой 2 – 4, проходящей через середины сторон AE и BC. От начала этой прямой N₂₄ по обе стороны вдоль основания картины откладывается натуральная величина радиуса окружности R и из полученных точек N_AB и N_CE проводятся прямые в точку схода P. Эти прямые являются полной перспективой прямых, на которых лежат стороны AB и CE. Для определения положения точек B и E через дистанционную точку D¹ и центр O^/ проводится прямая, на которой будет находиться диагональ квадрата BE (эта прямая имеет точку схода D¹, т.к. расположена под углом 45⁰ к картине). Полученная прямая отсекает на прямых N_ABP и N_CEP точки B^/ и E^/. Для получения вершин квадрата A^/ и C^/ достаточно из точек B^/ и E^/ провести прямые, параллельные основанию картины. Через точку O^/ также проводится прямая, параллельная основанию картины. Полученные точки 1^/, 2^/, 3^/, 4^/ являются серединами сторон квадрата A^/B^/C^/D^/ и, следовательно, точками касания его с окружностью. Для получения точек 5^/, 6^/, 7^/, 8^/, лежащих на диагоналях, в основании картины по обе стороны от точки N₂₄ откладывается расстояние 0,707R и через полученные точки проводятся прямые в главную точку P. Эти прямые пересекут диагонали в искомых точках. Далее эти восемь точек соединяются плавной кривой.

Удаление окружности от главной линии картины PP₀ приводит к значительному отклонению большой оси эллипса от горизонтального положения, что не соответствует зрительному восприятию окружности. Наиболее естественное восприятие окружности происходит, если ее центр находится на главной линии картины.

Для деления окружности на равное количество частей (например, на 12) строится другая окружность того же радиуса и с тем же центром, но в плоскости, параллельной картинной плоскости (рис.4.2). Эта окружность в перспективе также является окружностью, поэтому разделить ее на равные части не представляет труда. Из точек деления проводятся вертикальные прямые до пересечения с общим диаметром обеих окружностей A^/B^/. Если из полученных точек провести прямые в главную точку P, то они разделят исходную окружность на равные части.

При необходимости построения окружности, проходящей через заданную точку и концентрическую по отношению к заданной окружности, используется построение, основанное на рис.4.3.
Если через заданную точку A и центр заданной окружности O провести произвольную прямую AO, то отрезки 1 – 7; 3 – A; 6 – 4; 5 – 2 будут параллельны и, следовательно, иметь общую точку схода F¹. Прямая AO позволяет определить положение точек 3, 4, 6. Если провести еще одну прямую, то можно будет определить еще две точки на окружности. В качестве прямых аналогичных AO, можно использовать прямые, например, проходящие через точку O и главную точку P, или проходящие через точку O и дистанционные точки D¹ и D².

По заданной перспективе окружности, расположенной в горизонтальной плоскости, можно построить окружность в другой горизонтальной плоскости с таким же радиусом и центром на вертикальной прямой, проходящей через точку O^2/ (рис.4.4). Для этого через точки O^1/ и O^2/ проводятся параллельные горизонтальные прямые и определяется их точка схода. Вертикальная прямая, проведенная из точки пересечения нижней прямой с исходной окружностью 1^1/, пересекает верхнюю прямую в точке 1^2/, которая будет лежать на искомой окружности. Таким образом можно построить ряд точек. При этом удобно использовать прямые, которые имеют точку схода главную точку P и дистанционные точки D¹ и D².

По заданной перспективе горизонтальной окружности с центром в точке O^1/ можно построить перспективу другой горизонтальной окружности с центром в точке O^2/, расположенным на той же вертикали, что и точка O^1/, и проходящей через какую-либо заданную точку (например, точку 1^2/) (рис.4.5). Для этого через точку 1^2/ и точку O^2/ проводится прямая. На этой прямой будет находиться какой-то из диаметров искомой окружности, а ее точка схода F¹ (как для горизонтальной прямой) будет находиться на линии горизонта h. На прямой, проведенной из точки схода F¹ через точку O^2/, будет находиться диаметр заданной окружности 1^1/2^1/, параллельный диаметру искомой окружности, проходящему через точку 1^2/. Если через точки 1^1/ и 1^2/ провести прямую до пересечения с продолжением вертикали O^1/O^2/, то полученная точка S^/ будет вершиной конуса вращения, для которого обе окружности являются параллелями, а прямая 1^1/1^2/ – образующей. Прямая, проведенная через точки 2^1/ и S^/, также является образующей. Ее продолжение в пересечении с продолжением прямой 1^2/O^2/ даст точку 2^2/, лежащую на искомой окружности. Аналогичным образом можно построить ряд точек, лежащих на искомой окружности, кроме тех которые совпадают с вертикалью.

Задана окружность с центром в точке O^1/ и необходимо построить несколько окружностей того же радиуса с центрами в точках O^2/, O^3/ и т.д. (рис.4.6). Для этого малая ось эллипса выносится в сторону (на чертеже вправо), точки O, A и B соединяются с точкой O_h на линии горизонта. Величина вертикального отрезка CE, заключенного между полученными прямыми, является малой осью эллипса, являющегося проекцией окружности с центром в точке O^3/. Аналогичным образом можно построить перспективу любой окружности того же радиуса с центрами на той же вертикали. На этом чертеже можно наблюдать, так называемое, «раскрытие эллипсов».

Окружность, расположенная в плоскости, параллельной картинной, в перспективе также является окружностью. На рис.4.7 построен ряд соосных окружностей с центрами O^1/, O^2/, O^3/. Прямые 1^/P и 2^/P позволяют определить диаметры остальных окружностей по заданному диаметру 1 – 2.

Точкой схода горизонтальных сторон квадратов, описанных вокруг окружностей, является главная точка P (рис.4.8). Центры окружностей, а также соответствующие точки всех окружностей лежат на горизонтальных прямых, параллельных картинной плоскости. На рис.4.8 прослеживается «раскрытие» эллипсов, являющихся перспективой окружностей, лежащих в плоскостях, перпендикулярных картинной плоскости.

На рис.4.9 построена окружность с центром в точке O^2/ в плоскости, параллельной плоскости заданной окружности с центром в точке O^1/. Для этого построения достаточно провести вертикальные прямые из точек на вторичной проекции этой окружности до пересечения с параллельными прямыми, идущими из точек заданной окружности в совмещенную точку схода S^h.

Построению перспективы предшествует выбор точки зрения наблюдателя. Процесс выбора точки зрения требует комплексного учёта многих факторов и подразумевает выбор не только самой точки зрения, но и других параметров перспективы. Выбор точки зрения включает в себя следующие факторы:

1. Выбор положения точки стояния S₁ (выбор угла обзора α).
2. Выбор положения картинной плоскости K (выбор направления главного луча SP).
3. Выбор высоты линии горизонта h (выбор высоты точки зрения S).

Каждый из перечисленных факторов находится в определённой зависимости от двух других. Поэтому каждый из них выбирается исходя из определённых условий, а затем проверяется и при необходимости корректируется в соответствии со значениями остальных факторов. Ниже рассматривается выбор каждого фактора.

Выбирая положение точки стояния S₁ (рис. 5.1) на плане, необходимо учитывать, что угол ясного зрения α находится в пределах от 30° до 40°. В редких случаях разрешается использовать угол α до 50°. Выбор угла α равносилен выбору точки стояния S₁. Угол α измеряется между проецирующими лучами, проведенными из точки стояния S₁ к крайним точкам плана. Если главная точка P находится не точно в середине перспективного изображения, то вместо угла α необходимо учитывать угол β, составляющий большую из двух частей угла α, предъявляя к нему требования: β ≤ 15° – 20°. Уменьшение расстояния L от точки стояния до картинной плоскости влечет за собой увеличение угла β (или α). Проверку угла зрения необходимо осуществлять не только в горизонтальной, но и в вертикальной плоскости. Для этого из точки зрения проводится проецирующий луч к наиболее высокой и близкой точке сооружения (в данном случае к точке 2). Луч 2₁S₁ поворачивается вокруг точки 2₁ (как вокруг проецирующей оси) до положения фронтали, и строится его фронтальная проекция 2₂𝑺¯₂. Угол γ является аналогом угла β. Этим углом измеряется угол зрения в вертикальной плоскости. К углу γ предъявляются менее строгие требования: γ ≤ 40°. Это требование удовлетворяется, если расстояние L ≥ 2z, где z — расстояние от линии горизонта до наиболее удалённой точки сооружения, измеренное по вертикали. Расстояние z измеряется до верхней части сооружения, если линия горизонта находится низко, и, наоборот, до основания сооружения, если линия горизонта находится высоко. В отдельных случаях требуется проверить угол обзора в наклонной плоскости.
Положение картинной плоскости, параллельное основным граням сооружения, даёт перспективное изображение, называемое фронтальной перспективой. Положение картинной плоскости под углом к основным граням сооружения даёт перспективное изображение, называемое угловой перспективой. При этом картинная плоскость проводится через какую-либо вертикаль сооружения (обычно наиболее близкую к точке наблюдения). Углы φ и δ, образуемые картинной плоскостью с основными направлениями граней сооружения, должны заметно различаться. Угол δ, образуемый с главным фасадом, должен быть меньше угла φ, образуемого с боковым фасадом. Выбор картинной плоскости равнозначен выбору главного луча SP. При этом главная точка картины P не должна выходить за пределы средней трети картины (т. е. средней трети отрезка AB). Перемещение картинной плоскости вдоль главного луча не меняет изображение по существу. При этом изменяется только размер изображения.
Выбор высоты линии горизонта равносилен выбору высоты точки зрения и может осуществляться из различных соображений. Если при выборе точки зрения руководствуются соображениями ее реалистичности, то высота линии горизонта назначается примерно равной высоте человеческого роста с учетом рельефа местности. При разработке планировочных решений микрорайона и получении перспективы его в целом реальная точка зрения в большинстве случаев невозможна. В этом случае прибегают к построению перспективы с так называемой «высоты птичьего полета». При этом линия горизонта принимается значительно выше даже самых высоких зданий.
Последовательность выбора всех трёх факторов может быть разной. Например, можно сначала выбрать положение картинной плоскости, затем положение главной точки P на ней, что, в свою очередь, однозначно определяет направление главного луча. После этого назначается положение точки стояния и проверяются углы зрения в горизонтальной и вертикальной плоскостях.
При выборе точки обзора, помимо перечисленных выше ограничений, необходимо выполнить следующие требования: точка обзора должна быть реальной, перспектива, построенная с этой точки обзора, должна полностью раскрывать архитектурно-планировочное решение и авторский замысел.
Композиция изображения относительно листа бумаги также должна удовлетворять определенным требованиям:
а) сверху изображения должно быть больше свободного пространства, чем снизу, т. е. изображение должно располагаться ближе к нижней кромке листа бумаги;
б) при одинаково развитых фасадах изображение должно располагаться по горизонтали примерно посередине;
в) при разных фасадах больше свободного пространства оставляется со стороны более развитого фасада.

Построение перспективы может осуществляться различными методами, основой которых является аппарат центрального проецирования. Выбор метода построения зависит от многих условий и в каждом случае осуществляется исходя из конкретных условий поставленной задачи. С помощью выбранного метода строятся основные объемы перспективного изображения, а затем эти объемы детализируются с помощью различных способов (измерение отрезков, пропорциональное деление и т.д.).
В архитектурной практике используются следующие методы: метод архитектора, радиальный метод, метод совмещенных высот, метод координат, метод перспективной сетки.

Этот метод является наиболее часто используемым и может применяться в трех модификациях: способ с двумя точками схода, способ с одной точкой схода, способ вертикальной плоскости и опущенного плана. Ниже рассматривается каждый из этих способов.
Способ основывается на том, что архитектурные сооружения и их элементы в основном представляют собой параллелепипеды, горизонтальные ребра которых имеют два преимущественных направления с двумя точками схода, расположенными на линии горизонта. На рис.6.1 изображены два здания (два параллелепипеда, для которых построена угловая перспектива). Точка зрения выбрана согласно требованиям пункта 5. Точка F¹ является точкой схода для горизонтальных прямых 1 – 2, 3 – 4, 5 – 6, 7 – 8, а точка F² является точкой схода для прямых 1 – 4, 2 – 3, 5 – 8, 6 – 7. Построение перспективы начинается с построения перспективы основания параллелепипедов или плана, который является фактически вторичной перспективной проекцией верхних оснований этих параллелепипедов (рис.6.2). Для этого с горизонтальной проекции на основание перспективы переносятся точки пересечения проецирующих лучей с картинной плоскостью и основание главной точки (точки 6₀, 5₀, 2₀, 1₀, 4₀ и P₀ ). Перенос осуществляется с помощью засечек на ровной кромке полоски бумаги. Видимые вертикальные ребра параллелепипедов на перспективе будут совпадать с вертикальными прямыми, проведенными из этих точек. Точка 1(1₀), совмещенная с картинной плоскостью, является началом прямых 1 – 4 и 1 – 2, что позволяет соединить точку 1₀ с точками схода F¹ и F².
Вертикальные прямые, проведенные из точек 4₀ и 2₀, в пересечении с прямыми 1₀F² и 1₀F¹ дают положение точек 4 и 2. Прямые, проведенные из точек 4 и 2 в соответствующие точки схода, в пересечении дают точку 3. Вертикальная прямая из точки 5₀ в пересечении с продолжением прямой 2 – 3 дает точку 5. Прямая 5F¹ в пересечении с вертикальной прямой из точки 6₀ даст точку 6. Прямая 6F² в пересечении с прямой 4F¹ позволит получить точку 7. Таким образом построен перспективный план. Вертикальное ребро, проходящее через точку 1, находится в картинной плоскости и поэтому сохраняет свою натуральную величину, которая измеряется на фронтальной проекции и переносится на перспективу 11^/ – 1^/. Для построения верхнего основания малого параллелепипеда проводятся построения, аналогичные вышеописанным. Для построения большого параллелепипеда прямая 6^/₁ – 7^/₁ продлевается до основания картины. От полученной точки N₆₇, являющейся началом прямой 6^/₁ – 7^/₁, откладывается натуральная величина высоты большого параллелепипеда, т.к. она вынесена в картинную плоскость. Точка N^/₆₇ соединяется с точкой схода F², а вертикальные прямые из точек 6^/₁ и 7^/₁ отсекают на ней отрезок 6^/–7^/. Прямые, проведенные через точки 6^/ и 7^/ в точку схода F¹, в пересечении с вертикальными прямыми из точек 5^/₁ и 8^/₁ дают точки 5^/ и 8^/. Таким образом построены все вершины большого параллелепипеда. Последовательность построений может быть различной.

Перспектива, построенная с двумя точками схода, получается достаточно точной, а построения просты и не трудоемки. Недостатком этого способа является значительная удаленность одной из точек схода от перспективного изображения, что создает определенные трудности при построении. Способ с двумя точками схода используется на начальном этапе построения перспективы в виде предварительных эскизов.

При построении угловой перспективы одна из двух точек схода, оказывающаяся на значительном удалении, не используется (рис.6.3, 6.4) Вместо этого строятся начала всех прямых (N₅₈ ≡ N₂₃ и N₆₇), сходящихся в более близкую точку схода F₂, и на них вертикальными прямыми из оснований соответствующих точек отсекаются точки перспективного плана 5^/₁, 2^/₁, 3^/₁ ≡ 8^/₁, 6^/₁, 7^/₁. Вершины верхнего основания получаются в пересечении вертикалей из точек 1₀…8₀ с прямыми, идущими в точку схода F² из начала прямых верхнего основания. Начала этих прямых N^/₆₇, N^/₅₈, N^/₂₃ находятся над точками N₆₇, N₅₈ ≡ N₂₃ на высоте, равной натуральной высоте соответствующего параллелепипеда.

Способ построения перспективного изображения с одной точкой схода компактен. Однако, точность построения изображения меньшая по сравнению с предыдущим способом. Способ с одной точкой схода чаще всего используется для построения реальных перспектив зданий и архитектурных комплексов.

При низко расположенной линии горизонта перспективный план получается очень сжатым, что затрудняет построение перспективного изображения. Чтобы избежать этого вводится дополнительная горизонтальная предметная плоскость, которая располагается значительно ниже или выше заданной и строится перспективный план на новой предметной плоскости с той же самой линией горизонта с одной точкой схода.
Такой план называется соответственно опущенным или поднятым планом (рис.6.5, 6.6). Можно также сказать, что строится план на исходной предметной плоскости, но с завышенной линией горизонта. Далее вводится дополнительная вертикальная плоскость, которая пересечет картину по вертикальной прямой c, а исходную и введенную предметную плоскости по горизонтальным прямым a и a_оп соответственно с произвольной точкой схода F³. Положение этих прямых и точки схода F³ зависит от угла наклона вертикальной плоскости к картинной плоскости. Если эту плоскость задать перпендикулярно картине, то точка F³ совпадет с главной точкой картины, что не желательно, т.к. построения будут накладываться на основное изображение. С этой целью эта вертикальная плоскость выносится влево или вправо от изображения и располагается таким образом, чтобы точка схода F³ также находилась за пределами будущего изображения. На вертикальной прямой c от основания картины откладываются высоты основных объемов сооружения и из полученных точек проводятся прямые в точку схода F³. Из вершин опущенного плана проводятся горизонтальные прямые до пересечения с прямой a_оп. Из полученных точек проводятся вертикальные прямые до прямой a и до прямых соответствующего уровня по высоте. Из полученных точек проводят горизонтальные прямые, которые в пересечении с вертикальными прямыми из точек опущенного плана позволят получить перспективу основных объемов. Фактически перспектива строится через проекцию на введенную боковую вертикальную плоскость.

Иногда способ так и называют: способ опущенного плана и боковой стены. Как уже говорилось выше, способ используется при низкой линии горизонта, что встречается значительно чаще, т.к. естественная точка зрения находится на уровне человеческого роста.

Метод основан на том, что вертикальные размеры по мере удаления вглубь от картинной плоскости уменьшаются пропорционально горизонтальным размерам (рис.6.9). Например, для построения перспективы точки 8 достаточно измерить на фронтальной плоскости расстояние от точки 8₂ до линии горизонта z₈, затем отложить его на горизонтальной плоскости проекций от точки 8₁ параллельно картине, и полученную точку соединить с точкой зрения. Полученное расстояние z^/₈ между двумя радиальными лучами необходимо отложить на картине от линии горизонта вдоль вертикальной прямой, проходящей через точку 8₀. Полученная точка 8^/ является перспективой точки 8.
Для построения перспективного изображения этим методом нет необходимости в знании аппарата перспективы. Метод достаточно трудоемок и используется в случаях, когда объект имеет нерегулярную форму и использование каких-либо точек схода не целесообразно.

Метод основан на построении координат точек в перспективе (рис.6.11, 6.12). Для этого декартова система координат располагается таким образом, чтобы ось X совместилась с основанием картины, ось Z располагалась в плоскости картины, а ось Y, следовательно, была бы перпендикулярна картине. Таким образом, плоскость XOZ является картинной плоскостью, плоскость XOY является предметной плоскостью, а плоскость YOZ вертикальной плоскостью, перпендикулярной картине и предметной плоскости. В перспективе координатные оси изобразятся как на рис.6.12. Ось Y будет направлена в главную точку картины. Координаты точек откладываются следующим образом. Например, для построения перспективы точки 8 необходимо от начала координат O отложить вдоль оси X^/ координату x₈, измеренную на плане, и из полученной точки провести прямую в главную точку P. (Все точки на этой прямой имеют абсциссу x₈.) Далее также вдоль оси X^/ откладывается расстояние y₈, также измеренное на плане. Прямая, проведенная из этой точки в дистанционную точку D¹, отсечет на оси Y^/ перспективную ординату точки 8. Из полученной точки проводится горизонтальная прямая (все точки этой прямой имеют ординату y₈). Прямые y^/ = y₈ и x^/ = x₈ в пересечении дают точку 8^/₁, являющуюся вторичной перспективной горизонтальной проекцией точки 8. По оси Z^/ откладывается аппликата точки z₈, измеренная на фасаде. Из полученной точки проводится прямая в главную точку. Все точки этой прямой имеют аппликату z^/ = z₈. Прямая z^/ = z₈ в пересечении с вертикалью из точки y^/₈ дает вторичную перспективную вертикальную проекцию точки 8 на вертикальную плоскость. Пересечение вертикали из горизонтальной вторичной проекции и горизонтали из вертикальной вторичной проекции даст перспективную проекцию точки 8^/.
Описанный метод достаточно точный, но трудоемкий. Метод используется в случаях, когда невозможно построение точек схода и объект имеет нерегулярную структуру, т.е. в тех же случаях, что и способ совмещенных высот.

Метод основан на том, что на план наносится квадратная сетка, ориентированная таким образом, чтобы одно ее направление было параллельно картине, а другое – перпендикулярно (рис.6.13). Размеры квадратов принимаются кратными 1, 5 или 10 м в зависимости от размеров сооружения. Вершины квадратов вдоль основания картины нумеруется цифрами, а в направлении, перпендикулярном картине, обозначаются буквами, т.е. все вершины квадратов определяется сочетанием определенного числа и буквы. На фасаде наносятся высотные отметки сооружения. Далее сетка переносится в перспективу (рис.6.14). Линии сетки, параллельные картине, строятся через деления, полученные на нулевой прямой, перпендикулярной картине, с помощью дистанционной точки D¹. Линии сетки, перпендикулярные картине, сходятся в главной точке P. Затем с помощью визуального интерполирования строится перспективный план, т.е. переносятся на глаз точки сооружения, совпадающие с линиями сетки. Высоты построенных точек откладываются также с помощью сетки. Высоту точки, взятую с фасада, измеряют по горизонтали от вторичной проекции в перспективном масштабе и откладывают затем ее по вертикали (рис.6.14, точка A).
Способ перспективной сетки используется, когда сооружение имеет криволинейную форму, а также для построения планировочной перспективы, например, микрорайона. При использовании метода перспективной сетки линия горизонта должна находиться достаточно высоко («перспектива с высоты птичьего полета»), т.к. в противном случае перспективная сетка окажется сжатой и будет непригодна для использования.

Построение перспективы интерьера принципиально не отличается от построения перспективы экстерьера. Однако при этом имеются некоторые особенности. При нахождении внутри замкнутого помещения человеческий глаз за счет своего движения, а также движения головы, может охватить и увидеть большую часть внутреннего пространства. При построении линейной перспективы на картинную плоскость попадает далеко не все из того, что видит глаз. Кроме того, из-за замкнутости помещения реальная точка зрения оказывается на достаточно близком расстоянии от картинной плоскости, что увеличивает угол зрения до недопустимых величин. За счет этого перспектива оказывается значительно искаженной и не передает истинную картину интерьера. На рис.7.2а представлена фронтальная перспектива интерьера, построенная на картинной плоскости K¹ из точки зрения S¹ (рис.7.1).

Представленная перспектива создает впечатление излишней глубины помещения, чего нет в действительности. Чтобы устранить этот недостаток, можно было бы построить перспективу на цилиндрическую поверхность вращения с осью, совпадающей с точкой зрения и радиусом 1.5-2L. Однако это довольно трудоемко. Для перспективы интерьера такую цилиндрическую поверхность можно заменить призматической поверхностью, вписанной в цилиндрическую поверхность таким образом, чтобы ее ребра совпадали с проецирующими лучами, идущими от пересечения стен. Таким образом, цилиндрическая перспектива заменяется перспективой на несколько плоскостей, пересечение которых совпадает с линиями пересечения стен. Т.е. строится несколько линейных перспектив. Боковые перспективы разворачиваются и объединяются с фронтальной перспективой. Такая перспектива иногда называется театральной. На рис.7.2б представлена такая перспектива, построенная на картине K² при точке зрения S¹. На этой перспективе хорошо выявлено внутреннее пространство помещения, но ее построение достаточно трудоемко.
Хороший результат при построении перспективы интерьера дает использование нереальной (условной) точки зрения, расположенной за пределами помещения. На рис.7.2в построена перспектива на картинной плоскости K¹ и точке зрения S². Эта перспектива также хорошо отражает внутреннее пространство помещения, но строить ее значительно проще, чем предыдущую. Положение точки зрения S² выбирается из следующих соображений. Фронтальная плоскость картины K² ортогонально проецируется на картину K¹ (рис.7.1). Проецирующие лучи, проведенные из пересечения стен через точки проецирования A¹ и B¹, в пересечении с главным лучом позволят получить условную точку зрения S².
Выше рассматривалась фронтальная перспектива интерьера. Аналогичные рассуждения справедливы и для угловой перспективы интерьера. Для построения перспективы интерьера больших помещений (например, зрительных залов театров) используются методы построения широкоугольных перспектив.

Изображение теней придает перспективе дополнительную выразительность и объемность. Направление световых лучей в отличие от комплексного чертежа может быть произвольным. При этом возможны три случая расположения параллельных световых лучей, идущих от солнца: лучи направлены со стороны наблюдателя к объекту, лучи направлены со стороны объекта к наблюдателю, лучи параллельны картинной плоскости (фронтальное положение лучей). При этом угол наклона лучей может быть произвольным в каждом из этих случаев. Для построения теней в перспективе необходимо знать перспективную проекцию луча, а также его вторичную перспективную проекцию. На рис.8.1 – 8.3 показано построение теней на предметную плоскость от горизонтального отрезка в каждом из вышеперечисленных случаев. Параллельные лучи будут иметь общую точку схода. Точка схода вторичных проекций лучей F^т₁ находится на линии горизонта. Точка схода перспективной проекции лучей F^т в первом случае находится ниже линии горизонта (рис.8.1), во втором случае (рис.8.2) – выше линии горизонта, в третьем случае (рис.8.3) – точка схода отсутствует. Перспективная проекция тени A^т от точки A находится в пересечении вторичной проекции светового луча, направленного из вторичной проекции точки A^/₁ в точку схода F^т₁, с перспективной проекцией светового луча, направленного из точки A^/ в точку схода F^т. Аналогичным образом строится тень от точки B, что позволяет построить тень от отрезка по двум точкам.

Тень от горизонтальной прямой AB на горизонтальную плоскость также является горизонтальной прямой A^тB^т, которая параллельна исходному отрезку AB, и следовательно, имеет ту же точку схода F. Тень от вертикальной прямой на горизонтальную плоскость совпадает с направлением вторичной проекции светового луча (рис.8.4).
На практике чаще всего используется первый случай направления световых лучей, т.к. большая часть объекта в этом случае освещена, и перспектива выглядит наиболее выразительно.
Из всех способов построения теней, известных по теням на комплексном чертеже, в перспективе используются только два: способ лучевых сечений и способ обратных лучей. Остальные способы не используются, т.к. приводят к сложным построениям.
Последовательность построения теней такая же, как и на комплексном чертеже: выявляется контур собственной тени, затем строится падающая тень от контура собственной тени каждого геометрического образа на предметную плоскость (на комплексном чертеже на стену), затем падающие тени от одного геометрического образа на другой.

На рис.8.5 показано построение теней на примере двух параллелепипедов. От контура собственной тени 1^/₁ – 1^/ – 2^/ – 3^/ – 3^/₁ – 2^/₁ – 1^/₁ малого параллелепипеда построена тень на предметную плоскость как от вертикальных и горизонтальных прямых. Затем построена тень от контура собственной тени 4^/₁ – 4^/ – 5^/ – 6^/ – 6^/₁ – 5^/₁ – 4^/₁ большого параллелепипеда на предметную плоскость. Контуром падающей тени обоих параллелепипедов является огибающий контур обеих теней. Кроме того, тень от большого параллелепипеда падает на верхнюю горизонтальную и переднюю вертикальную грани малого параллелепипеда. Для получения этой тени строятся лучевые сечения малого параллелепипеда, полученные от пересечения лучевых плоскостей, проведенных через контур собственных теней большого параллелепипеда. Такая лучевая плоскость проведена через ребро 4^/ – 4^/₁ большого параллелепипеда, и она пересекла малый параллелепипед по сечению, которое является контуром падающей тени. Другие участки собственной тени большого параллелепипеда дают тени только на предметную плоскость. На рис.8.6 построены тени от тех же параллелепипедов при фронтальном положении лучей.

Дополнительную выразительность и наглядность перспективному изображению придают не только тени, но и отражения на зеркальной поверхности, поверхности воды, полированных поверхностях пола и т.д.
Построение отражений основывается на известном положении о том, что угол отражения светового луча равен углу его падения (рис.9.1). Отражение точки A на горизонтальной отражающей плоскости строится следующим образом. От вторичной перспективной проекции A^/₁ точки A на горизонтальную отражающую плоскость откладывается по вертикали расстояние A^/₁A^/ в сторону, противоположную от точки A^/. Полученная точка A^/_от является отражением точки A^/ (рис.9.1).

Отражения вертикальных прямых в перспективе также являются вертикальными прямыми. Отражения горизонтальных прямых являются горизонтальными прямыми с теми же точками схода (рис.9.2). Отражения наклонных прямых имеют точки схода на одной вертикали с точками схода исходных прямых на таком же расстоянии от линии горизонта, но в противоположную сторону. Отражения контуров теней строятся по тем же принципам, что и обычных линий (рис.9.3).
В случае, если отражающая горизонтальная плоскость не совпадает с предметной плоскостью, строится часть перспективного плана на уровне отражающей плоскости, и расстояния по вертикали для видимого контура сооружения откладываются от точек этого плана в противоположную сторону (рис.9.4).

Отражения на горизонтальных поверхностях могут быть на зеркальной поверхности воды или полированного пола в интерьере. На вертикальных плоскостях отражения могут возникать в зеркалах стен интерьеров. Принципы построения отражений в вертикальных плоскостях такие же, как и на горизонтальной плоскости: необходимо по другую сторону от отражающей плоскости отложить те же расстояния, что и до нее. Причем в профильной плоскости эти расстояния действительно одинаковые (по оси X), а на фронтальной отражающей плоскости одинаковые в перспективе (по оси Y) и строятся с помощью прямой, проведенной из вершины профильного прямоугольника через середину противоположной вертикальной стороны до пересечения с продолжением горизонтальной стороны (рис.9.5).

При построении перспективы высокого сооружения и близко расположенной точке зрения угол зрения γ в вертикальной плоскости может стать недопустимо большим при вполне приемлемом угле зрения в горизонтальной плоскости. В таких случаях строится линейная перспектива на наклонной плоскости. При этом плоскость наклонена на зрителя, если линия горизонта находится низко и, наоборот, плоскость наклонена от зрителя, если линия горизонта находится высоко (рис.10.1).
При построении перспективы на наклонную плоскость возникает третья точка схода F³ для вертикальных прямых. Положение точки F³ определяется следующим образом: из точки зрения проводится вертикальная прямая до пересечения с картиной, картинная плоскость K¹ поворачивается вокруг своего основания до совмещения с вертикальной плоскостью K, точка F³ будет находиться на главной линии картины. Главная точка картины P будет находиться выше линии горизонта, а точка P_h, находящаяся на линии горизонта называется главной точкой горизонта. На основание картины обычным способом переносятся основания точек схода F¹₀ и F²₀, а также точки пересечения проецирующих лучей из характерных точек плана здания (1₀, 2₀, 3₀, 4₀) с основанием картины. Пересечение прямых, проведенных из точек F¹₀ и F²₀ в точку схода F³, с линией горизонта позволяет получить точки схода горизонтальных прямых F¹ и F². Далее обычным способом строится перспективный план, все вертикальные прямые проводят через точки на основании картины 1₀, 2₀, 3₀, 4₀ и точку схода F³. От точки 1₀ откладывают высоту ребра, измеренную на наклонной плоскости. Остальные ребра получаются по построению. Построения достаточно просты, однако требуют наличия всех трех точек схода.

Вертикальная точка схода обычно может оказаться достаточно далеко. Поэтому часто используется другой способ, позволяющий вести построения без использования точек схода (рис.10.2). Этот способ компактен, но менее точен. Суть способа заключается в том, что на картину переносится не только ряд точек пересечения проецирующих лучей с основанием картины, но и пересечения проецирующих лучей с картиной на каком-либо уровне, например, верха сооружения. Переносится также пересечение проецирующих лучей с картиной с фронтальной проекции. При соединении соответствующих точек двух горизонтальных рядов получаются вертикальные прямые, которые в пересечении с горизонтальными прямыми дают точки вершин здания.

Аналогично тому, как по аксонометрической проекции можно построить комплексный чертеж, также комплексный чертеж можно восстановить по перспективному изображению. Такой процесс восстановления называется реконструкцией перспективы. Реконструкция перспективы подразумевает не только построение комплексного чертежа, но и определение положения точки зрения (положение точки зрения, картинной плоскости и линии горизонта).
Задача реконструкции перспективы может возникнуть в следующих случаях:

• при реставрационных работах по сохранившимся фотографиям или другим перспективным изображениям;
• при создании первоначального эскизного перспективного изображения будущего проекта;
• при невозможности выполнения обмерных работ на объекте и замена их реконструкцией перспективы по фотографии.

В любом из перечисленных случаев реконструкция перспективы может быть осуществлена лишь с точностью до подобия, так как заранее не известна степень уменьшения изображения по отношению к оригиналу. Поэтому, чтобы реконструкция считалось полной, необходимо знать натуральную величину какого-либо объекта на перспективном изображении.
В архитектурной проектной практике часто возникает вопрос о том, как будет выглядеть проектируемое здание или сооружение в существующей окружающей среде. С этой целью необходимо вписать изображение будущего здания в фотографию реальной среды. Решение такой задачи называется фотомонтажом.

Произвести реконструкцию перспективы достаточно просто, если на перспективе имеется изображение квадрата, или окружности, или прямоугольника с известным соотношением сторон. При этом они должны лежать в горизонтальных или вертикальных плоскостях.
В случае окружности вокруг нее всегда можно описать квадрат. В случае прямоугольника с известным соотношением сторон путём пропорционального деления также можно выделить квадрат.
На рис. 11.1 представлено перспективное изображение четырехугольника ABCE, о котором известно, что это квадрат, лежащий в горизонтальной плоскости. Продолжая его стороны, можно найти точки схода его сторон F¹ и F². Прямая, проведенная через точки F¹ и F², будет горизонтальной прямой, являющейся линией горизонта h. Продолжение биссектрисы AC даст точку схода биссектрисы F_бис.
На горизонтальной проекции, находящейся в проекционной связи с перспективой, построена картинная плоскость K₁. На нее перенесены точки схода F¹, F², F_бис и основания вершин квадрата A₀, B₀, C₀, E₀. На отрезке F¹F² как на диаметре построена окружность и проведен еще один диаметр 12, перпендикулярный диаметру F¹F². Продолжение прямой 1F_бис пересечет эту окружность в точке S₁. Углы 1S₁F¹ и 1S₁F² равны 45° как вписанные углы, опирающиеся на дуги в 90°. Отрезок S₁F_бис является биссектрисой угла F¹S₁F², который является прямым как опирающийся на диаметр. Следовательно, точка S является точкой зрения, а прямые S₁F¹ и S₁F² параллельны направлениям сторон квадрата. Прямые из точки A, параллельные S₁F¹ и S₁F², в пересечении с продолжениями прямых из точки зрения S, проведенными через точки B₀ и E₀ соответственно, дадут горизонтальные проекции точек B₁ и E₁. Две другие стороны квадрата строятся параллельно AB и AE и в пересечении дают вершину квадрата C₁. Перпендикуляр из точки S₁ на картинную плоскость даст положение главной точки P (на чертеже не показано).

На рис. 11.2 показано определение натуральной величины стороны квадрата при уже известных из предыдущей задачи положении точки зрения S и главной точки P. От точки P по вертикали откладывается расстояние от точки зрения до картины для получения совмещенной точки зрения S_c. Дуги из точек F¹ и F² радиусами F¹S_c и F²S_c соответственно в пересечении с линией горизонта дадут точки измерения M¹ и M². Прямые из точек M¹ и M² через точки B и E отсекут в основании картины натуральные величины сторон квадрата с точностью до подобия.

На рис. 11.3 показан пример реконструкции перспективы с точностью до подобия здания с окружностью в вертикальной плоскости. Основание картины k проведено через точку A^|. Продолжения горизонтальных ребер здания позволяют построить точки схода F¹ и F², линию горизонта h. Построенный вокруг окружности квадрат имеет одну из сторон в картинной плоскости, что дает её натуральную величину с точностью до подобия. Отложив ее от точки A^| вдоль основания картины и проведя из полученной точки прямую через точку E^| до пересечения с линией горизонта, можно получить точку измерения M². Дуга из точки схода F² радиусом F²M² до пересечения с окружностью диаметром F¹F² дает совмещенную точку зрения S_c, а следовательно, и главную точку P. Дуга из точки схода F¹ радиусом F¹S_c до пересечения с линией горизонта дает точку измерения M¹ для прямых, сходящихся в точке схода F¹. Прямая, проведенная из точки измерения M¹ через точку B^|, отсечет в основании картины натуральную величину отрезка AB. На горизонтальной плоскости проекций, расположенной в проекционной связи с перспективой, можно построить план здания аналогично задаче на рис. 11.1. Фасад здания построен в проекционной связи с планом с использованием натуральной величины вертикального ребра.

Для того, чтобы провести полную реконструкцию перспективы, необходимо знать реальный линейный размер какого-либо объекта. Лучше всего, если это будет вертикальный размер, так как в этом случае любая точка на линии горизонта может стать точкой измерения. С её помощью вертикальный элемент выносится в картинную плоскость, где измеряется его величина и соотносится с реальной натуральной величиной объекта и тем самым определяется степень (масштаб) уменьшения перспективы (рис. 11.4). На перспективе такими объектами, вертикальный размер который известен, могут быть изображение человека, или другие объекты, размеры которых по разным причинам известны.
При реконструкции перспективы с точностью до подобия основание картины можно назначать произвольно. При этом перенос основания картины на перспективе влечёт за собой перемещение картинной плоскости параллельно самой себе, то есть вдоль главного луча. Это никак не отразится на самом изображении, отразится только на степени его увеличения, или уменьшения.
При полной реконструкции перспективы основание картины должно остаться в том же месте как при реконструкции с точностью до подобия. В противном случае невозможно будет определить действительную степень уменьшения перспективы. Если считать средний рост человека примерно 1.7 м, а на чертеже это соответствует, например ~ 12 мм, то степень уменьшения перспективы равна приблизительно 1:140. Поэтому комплексный чертеж построен в нестандартном масштабе М1:140 (рис. 11.4).

В фотографию существующей застройки требуется вписать рекламный щит. Для этого необходимо решить задачу реконструкции перспективы, а именно, определить возможные точки схода, положение линии горизонта, точек измерения, совмещенной точки зрения, степень уменьшения перспективного изображения.
На рис. 11.5 показан пример построения рекламного щита размерами 1500х1000 мм с одной стороной, параллельной главному фасаду существующего здания. Место вставки щита задано в точке A.
По горизонтальным направлениям определяется точка схода F¹ и линия горизонта h. Основание картины k совмещается с нижней кромкой фотографии. Если фотография не подвергалась кадрированию, то главная точка P находится точно на серединной вертикали. Поэтому для ее нахождения из точки пересечения диагоналей прямоугольника фотографии опускается перпендикуляр на линию горизонта.
На фотографии имеется квадратная крышка люка и колесо автомобиля, реальные размеры которых могут быть определены.
С помощью биссектрисы квадрата крышки определяется положение совмещенной точки зрения S_c, а затем и второй точки схода F². Определяется положение точек измерения M¹ и M², которые в свою очередь, дают возможность определить натуральную величину стороны квадрата a с точностью до подобия. Эта величина a соответствует стандартному размеру люка, равную 700 мм. То есть степень уменьшения перспективы n=700/a. Еще проще было бы воспользоваться натуральной величиной диаметра колеса автомобиля при возможности определения его модели.
Используя любую точку на линии горизонта в качестве точки измерения, по вертикали откладываются размеры высоты тротуара (на чертеже величина не показана), стойки b=500/n и щита c=1000/n. Используя точку измерения M¹, по горизонтали в основании картины симметрично относительно вынесенной точки A, откладывается горизонтальный размер щита d=1500/n. С помощью точек схода строится изображение щита.

Ниже приводятся примеры построения архитектурных форм: арки и карниза