РАЗДЕЛ I. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Онлайн-учебник
1. ВВЕДЕНИЕ
С древнейших времён человечество пыталось отобразить окружающий мир в виде изображений на поверхности каких-либо материалов. В разное время в качестве таких поверхностей могли выступать гладкие поверхности скал, кожа, пергамент, береста, камень, дерево и, наконец, бумага. Эти изображения несли в себе графическую информацию, которую можно было передавать друг другу и, что особенно ценно, следующим поколениям. Осознанно или неосознанно графические изображения создавались с помощью методов проецирования. Все графические изображения можно разделить на два вида. К первому из них относятся рисунок и живопись, ко второму — чертёж. Несмотря на то, что оба вида изображений получены методами проецирования, между ними есть существенная разница, которая заключается в следующем. В рисунке или живописной картине автор отображает собственное видение и индивидуальное восприятие окружающего мира. И это замечательно, потому что рисунок и живопись — это искусство. В отличие от художественного рисунка, чертёж не должен нести в себе никаких черт индивидуального восприятия, а должен быть выполнен по определённым законам и правилам, чтобы восприниматься абсолютно одинаково, независимо от того, кто его выполнил или кто использовал его в работе.
Предметом изучения начертательной геометрии являются методы построения чертежей. Задолго до того, как начертательная геометрия оформилась как наука, человечество уже пользовалось чертежами. Однако эти чертежи представляли собой смесь рисунка и чертежа в современном понимании.
Основателем начертательной геометрии по праву считается великий французский учёный и политический деятель Гаспар Монж. Именно он заложил теоретические основы начертательной геометрии в том виде, в котором мы пользуемся ими до сих пор.
Основной целью изучения начертательной геометрии в вузе является освоение закономерностей, по которым строятся графические изображения методами проецирования, а также развитие пространственного мышления у студентов.
Предметом изучения начертательной геометрии являются методы построения чертежей. Задолго до того, как начертательная геометрия оформилась как наука, человечество уже пользовалось чертежами. Однако эти чертежи представляли собой смесь рисунка и чертежа в современном понимании.
Основателем начертательной геометрии по праву считается великий французский учёный и политический деятель Гаспар Монж. Именно он заложил теоретические основы начертательной геометрии в том виде, в котором мы пользуемся ими до сих пор.
Основной целью изучения начертательной геометрии в вузе является освоение закономерностей, по которым строятся графические изображения методами проецирования, а также развитие пространственного мышления у студентов.
2. ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ
С точки зрения начертательной геометрии предметы окружающего нас мира являются геометрическими образами. Абстрагируясь, их можно свести к трём геометрическим образам: точке, линии и поверхности. Точка — это геометрический образ, не имеющий размеров. В результате движения точки по какой-либо траектории образуется геометрический образ, называемый линией, то есть линия — это траектория движения точки. Линия имеет одно измерение — это её длина. В результате движения линии образуется геометрический образ, называемый поверхностью, то есть поверхность — это траектория движения линии по определённому закону. Поверхность имеет два измерения. Плоскость является частным случаем поверхности. Поверхность считается не имеющей толщины, но при этом непрозрачной. Способ получения геометрических образов путём движения какого-либо другого геометрического образа называется кинематическим способом.
В данном курсе начертательной геометрии для обозначения геометрических образов на чертеже вводятся следующие обозначения. Для точек вводится обозначение в виде заглавных букв латинского алфавита (A, B, C …). Линии обозначаются строчными буквами латинского алфавита (a, b, c …). Поверхности обозначаются заглавными буквами греческого алфавита (например, Δ, Γ, Σ, Φ …).
В данном курсе начертательной геометрии для обозначения геометрических образов на чертеже вводятся следующие обозначения. Для точек вводится обозначение в виде заглавных букв латинского алфавита (A, B, C …). Линии обозначаются строчными буквами латинского алфавита (a, b, c …). Поверхности обозначаются заглавными буквами греческого алфавита (например, Δ, Γ, Σ, Φ …).
3. МЕТОДЫ ПРОЕЦИРОВАНИЯ




Основой аппарата получения графических изображений является проецирование. Понятие проецирования встречается в нашей повседневной жизни независимо от нас. Например, тени предметов, отражения в зеркале или на поверхности воды — это проекции, созданные самой природой. В начертательной геометрии при построении изображений используются следующие методы проецирования: метод центрального проецирования, метод параллельного проецирования, метод прямоугольного или ортогонального проецирования.
Метод центрального проецирования. Точки A, O и плоскость Π1 находятся в пространстве. Если из точки O провести луч через точку A до пересечения с плоскостью Π1, то точка A1 пересечения луча с плоскостью Π1 называется проекцией точки A на плоскость Π1 (рис. 3.1). При этом точка O называется центром проецирования; луч, исходящий из точки O, называется проецирующим лучом; плоскость Π1 называется плоскостью проецирования. Такое проецирование называется центральным.
Метод центрального проецирования. Точки A, O и плоскость Π1 находятся в пространстве. Если из точки O провести луч через точку A до пересечения с плоскостью Π1, то точка A1 пересечения луча с плоскостью Π1 называется проекцией точки A на плоскость Π1 (рис. 3.1). При этом точка O называется центром проецирования; луч, исходящий из точки O, называется проецирующим лучом; плоскость Π1 называется плоскостью проецирования. Такое проецирование называется центральным.
Для того, чтобы получить проекцию отрезка прямой линии, достаточно спроецировать две его точки. Тогда центральной проекцией отрезка BC на плоскость Π1 будет являться отрезок прямой линии B1C1 (рис.3.1).
Методом центрального проецирования строятся перспективные изображения. Зрительные органы человека воспринимают окружающий мир на сетчатке глаза по принципам центрального проецирования. Поэтому наиболее наглядными изображениями являются изображения, полученные по методу центрального проецирования.
Метод параллельного проецирования. В случае если центр проекций O удалить в бесконечность, проецирующие лучи станут параллельными определенному направлению и друг другу. Такой способ проецирования называется параллельным (рис.3.2). В этом случае отрезок прямой B1C1 называется параллельной проекцией отрезка BC на плоскость проекций Π1.
Параллельное проецирование является частным случаем центрального проецирования, когда центр проекций удален в бесконечность.
Метод ортогонального (прямоугольного) проецирования. В случае, если параллельные проецирующие лучи перпендикулярны плоскости проекций, то метод проецирования называется прямоугольным или ортогональным. Проекции, полученные таким методом, называются ортогональными или прямоугольными проекциями (рис.3.3).
Методом центрального проецирования строятся перспективные изображения. Зрительные органы человека воспринимают окружающий мир на сетчатке глаза по принципам центрального проецирования. Поэтому наиболее наглядными изображениями являются изображения, полученные по методу центрального проецирования.
Метод параллельного проецирования. В случае если центр проекций O удалить в бесконечность, проецирующие лучи станут параллельными определенному направлению и друг другу. Такой способ проецирования называется параллельным (рис.3.2). В этом случае отрезок прямой B1C1 называется параллельной проекцией отрезка BC на плоскость проекций Π1.
Параллельное проецирование является частным случаем центрального проецирования, когда центр проекций удален в бесконечность.
Метод ортогонального (прямоугольного) проецирования. В случае, если параллельные проецирующие лучи перпендикулярны плоскости проекций, то метод проецирования называется прямоугольным или ортогональным. Проекции, полученные таким методом, называются ортогональными или прямоугольными проекциями (рис.3.3).
В дальнейшем в настоящем курсе начертательной геометрии используется метод ортогонального проецирования.
Обратимость чертежа. Проекции, полученные вышеописанными методами проецирования на одну плоскость проекций, не обладают свойством обратимости или однозначности чертежа. Это свойство заключается в том, что при проецировании на одну плоскость проекций можно получить проекцию оригинала геометрического образа, расположенного в пространстве. При этом, имея одну проекцию геометрического образа, невозможно восстановить однозначно положение оригинала геометрического образа в пространстве. Например, проекция отрезка CD (C1D1) совпадает с проекцией отрезка AB (A1B1). Поэтому по этой проекции невозможно судить о каком отрезке в пространстве идет речь (рис.3.4). Это утверждение относится ко всем трем методам проецирования.
Обратимость чертежа. Проекции, полученные вышеописанными методами проецирования на одну плоскость проекций, не обладают свойством обратимости или однозначности чертежа. Это свойство заключается в том, что при проецировании на одну плоскость проекций можно получить проекцию оригинала геометрического образа, расположенного в пространстве. При этом, имея одну проекцию геометрического образа, невозможно восстановить однозначно положение оригинала геометрического образа в пространстве. Например, проекция отрезка CD (C1D1) совпадает с проекцией отрезка AB (A1B1). Поэтому по этой проекции невозможно судить о каком отрезке в пространстве идет речь (рис.3.4). Это утверждение относится ко всем трем методам проецирования.
4. ОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА


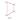

Для устранения неоднозначности чертежа, получаемого проецированием на одну плоскость проекций, Г. Монж предложил проецировать на две плоскости проекций (рис.4.1). При этом плоскость проекций Π1 принято считать горизонтальной, а вторую плоскость проекций Π2 располагать перпендикулярно первой и называть ее фронтальной. Проекции геометрических образов на плоскости проекций должны иметь те же индексы, что и плоскости проекций, и называться соответственно горизонтальной и фронтальной проекцией геометрического образа.
Величина длины отрезка в пространстве (натуральная величина) при проецировании искажается. При прямоугольном проецировании длина проекции отрезка всегда меньше (или равна) натуральной величине отрезка в пространстве. Для ее нахождения необходимо рассмотреть прямоугольный треугольник ABA/, в котором натуральная величина отрезка является гипотенузой (рис.4.4, 4.5).
Для определения величины гипотенузы достаточно построить катеты этого прямоугольного треугольника, которыми являются величина одной из проекций, например, A1B1 и величина разницы по высоте между точками A и B. Эту разницу можно взять с другой плоскости проекций A2A2/. Аналогичным образом можно построить другой прямоугольный треугольник, который образуется при проецировании на фронтальную плоскость проекций. При этом одним из катетов будет фронтальная проекция отрезка A2B2, а вторым катетом является расстояние, которым определяется то, насколько одна точка ближе (или дальше) другой. Это расстояние измеряется на горизонтальной плоскости проекций. Таким образом, можно построить два разных прямоугольных треугольника, но гипотенуза у них будет одинаковая по величине и равная натуральной величине отрезка. Эти треугольники можно построить на комплексном чертеже, начертив второй катет непосредственно к проекции, являющейся первым катетом. При этом необходимо помнить, что приведенные построения не являются элементами комплексного чертежа, а всего лишь позволяют определить натуральную величину отрезка.
При проецировании искажаются не только длины отрезков, но и величины углов. Произвольный по величине угол между двумя прямыми линиями проецируется в натуральную величину на плоскость проекций, если его стороны параллельны плоскости проекций. В отличие от произвольного угла, прямой угол проецируется в натуральную величину на плоскость проекций, если хотя бы одна из его сторон параллельна этой плоскости проекций (это можно доказать, используя теорему о трех перпендикулярах). Последнее утверждение носит название теоремы о проецировании прямого угла.
Для определения величины гипотенузы достаточно построить катеты этого прямоугольного треугольника, которыми являются величина одной из проекций, например, A1B1 и величина разницы по высоте между точками A и B. Эту разницу можно взять с другой плоскости проекций A2A2/. Аналогичным образом можно построить другой прямоугольный треугольник, который образуется при проецировании на фронтальную плоскость проекций. При этом одним из катетов будет фронтальная проекция отрезка A2B2, а вторым катетом является расстояние, которым определяется то, насколько одна точка ближе (или дальше) другой. Это расстояние измеряется на горизонтальной плоскости проекций. Таким образом, можно построить два разных прямоугольных треугольника, но гипотенуза у них будет одинаковая по величине и равная натуральной величине отрезка. Эти треугольники можно построить на комплексном чертеже, начертив второй катет непосредственно к проекции, являющейся первым катетом. При этом необходимо помнить, что приведенные построения не являются элементами комплексного чертежа, а всего лишь позволяют определить натуральную величину отрезка.
При проецировании искажаются не только длины отрезков, но и величины углов. Произвольный по величине угол между двумя прямыми линиями проецируется в натуральную величину на плоскость проекций, если его стороны параллельны плоскости проекций. В отличие от произвольного угла, прямой угол проецируется в натуральную величину на плоскость проекций, если хотя бы одна из его сторон параллельна этой плоскости проекций (это можно доказать, используя теорему о трех перпендикулярах). Последнее утверждение носит название теоремы о проецировании прямого угла.

5. ЗАДАНИЕ ПРЯМЫХ ЛИНИЙ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
5.1. Положение прямых относительно плоскостей проекций

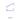

Прямая линия относительно плоскостей проекций может располагаться следующим образом: прямая занимает произвольное положение, прямая параллельна плоскости проекций, прямая параллельна обеим плоскостям проекций, прямая перпендикулярна какой-либо плоскости проекций. Ниже рассматривается каждый из этих случаев.
1. Прямая, расположенная в пространстве произвольным образом, носит название прямой общего положения. Ее проекции могут располагаться произвольно (рис.5.1).
1. Прямая, расположенная в пространстве произвольным образом, носит название прямой общего положения. Ее проекции могут располагаться произвольно (рис.5.1).
2. Прямая, параллельная горизонтальной плоскости проекций, называется горизонталью, обозначается буквой h, проецируется на горизонтальной плоскости проекций в натуральную величину, а на фронтальной плоскости в виде прямой, перпендикулярной линиям связи (рис.5.2).
3. Прямая, параллельная фронтальной плоскости проекций, называется фронталью, обозначается буквой f, проецируется на фронтальной плоскости проекций в натуральную величину, а на горизонтальной плоскости в виде прямой, перпендикулярной линиям связи (рис.5.3).
4. Прямая, перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей, ее горизонтальная проекция вырождается в точку, а фронтальная проекция совпадает с линией связи (рис.5.4).
3. Прямая, параллельная фронтальной плоскости проекций, называется фронталью, обозначается буквой f, проецируется на фронтальной плоскости проекций в натуральную величину, а на горизонтальной плоскости в виде прямой, перпендикулярной линиям связи (рис.5.3).
4. Прямая, перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей, ее горизонтальная проекция вырождается в точку, а фронтальная проекция совпадает с линией связи (рис.5.4).
5. Прямая, перпендикулярная фронтальной плоскости проекций, называется фронтально проецирующей, ее фронтальная проекция вырождается в точку, а горизонтальная проекция совпадает с линией связи (рис.5.5).
6. Прямая, параллельная одновременно обеим плоскостям проекций, называется профильно проецирующей прямой и ее обе проекции перпендикулярны линиям связи (рис.5.6).
7. Прямая, параллельная профильной плоскости проекций, называется профильной прямой и ее обе проекции совпадают с линиями связи (рис.5.7).
Профильной плоскостью проекций называется третья плоскость проекций, которая перпендикулярна одновременно горизонтальной и фронтальной плоскостям проекций, обозначается Π3 и иногда используется в построениях.
Профильная проекция соответствует взгляду слева на геометрический образ.
Все перечисленные прямые, кроме прямых общего положения, объединяются общим названием прямые частного положения. Фронталь, горизонталь и профильная прямая объединяются общим названием прямые уровня.
6. Прямая, параллельная одновременно обеим плоскостям проекций, называется профильно проецирующей прямой и ее обе проекции перпендикулярны линиям связи (рис.5.6).
7. Прямая, параллельная профильной плоскости проекций, называется профильной прямой и ее обе проекции совпадают с линиями связи (рис.5.7).
Профильной плоскостью проекций называется третья плоскость проекций, которая перпендикулярна одновременно горизонтальной и фронтальной плоскостям проекций, обозначается Π3 и иногда используется в построениях.
Профильная проекция соответствует взгляду слева на геометрический образ.
Все перечисленные прямые, кроме прямых общего положения, объединяются общим названием прямые частного положения. Фронталь, горизонталь и профильная прямая объединяются общим названием прямые уровня.


5.2. Взаимное положение прямых

Две прямые относительно друг друга могут располагаться следующим образом: быть параллельными, пересекаться, скрещиваться. Ниже рассматривается каждый из этих случаев.
1. Две прямые параллельны друг другу, если их одноименные проекции параллельны (одноименные проекции – это проекции на одну и ту же плоскость проекций, т.е. проекции с одинаковыми индексами) (рис.5.8).
2. Две прямые пересекаются, если у них имеется общая точка, проекции которой лежат на одной линии связи (рис.5.9).
3. Две прямые скрещиваются, если они не параллельны и не пересекаются. Это возможно, если прямые не параллельны, но лежат в параллельных плоскостях (рис.5.10).
1. Две прямые параллельны друг другу, если их одноименные проекции параллельны (одноименные проекции – это проекции на одну и ту же плоскость проекций, т.е. проекции с одинаковыми индексами) (рис.5.8).
2. Две прямые пересекаются, если у них имеется общая точка, проекции которой лежат на одной линии связи (рис.5.9).
3. Две прямые скрещиваются, если они не параллельны и не пересекаются. Это возможно, если прямые не параллельны, но лежат в параллельных плоскостях (рис.5.10).
В случае скрещивающихся прямых возникает вопрос о видимости совпадающих (конкурирующих) точек. В данном случае конкурирующими являются точки 1 и 2, а также точки 3 и 4. Точка 1, принадлежащая прямой a, совпадает на фронтальной плоскости проекций с точкой 2, принадлежащей прямой b. При переходе на горизонтальную плоскость проекций обнаруживается, что точка 2 расположена ближе, а точка 1 – дальше от наблюдателя. Поэтому на фронтальной плоскости проекций точка 2 заслонит точку 1 (поэтому точка 1 заключена в скобки). Рассуждая аналогичным образом относительно конкурирующих точек 3 и 4 на горизонтальной плоскости проекций и, перейдя на фронтальную плоскость проекций, обнаруживается, что точка 3, принадлежащая прямой a, расположена выше точки 4, принадлежащей прямой b. Поэтому на горизонтальной плоскости проекций, т.е. при взгляде сверху, из двух конкурирующих точек 3 и 4 будет видна точка 3.
Анализ видимости на комплексном чертеже более сложных геометрических образов в любом случае сводится к анализу видимости каких-либо конкурирующих точек, принадлежащих этим образам. При этом видимость на фронтальной плоскости проекций определяется по взаимному положению точек на горизонтальной плоскости проекций, видимость на горизонтальной плоскости проекций определяется по взаимному положению точек на фронтальной плоскости проекций.
Анализ видимости на комплексном чертеже более сложных геометрических образов в любом случае сводится к анализу видимости каких-либо конкурирующих точек, принадлежащих этим образам. При этом видимость на фронтальной плоскости проекций определяется по взаимному положению точек на горизонтальной плоскости проекций, видимость на горизонтальной плоскости проекций определяется по взаимному положению точек на фронтальной плоскости проекций.

6. ЗАДАНИЕ ПЛОСКОСТИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ

Плоскость на комплексном чертеже можно задать следующими способами:
1. Тремя точками, не лежащими на одной прямой (рис.6.1).
2. Прямой и точкой, не лежащей на этой прямой (рис.6.2).
3. Двумя пересекающимися прямыми (рис.6.3).
4. Двумя параллельными прямыми (рис.6.4).
5. Любой плоской кривой или ломаной линией (например, треугольником) (рис.6.5).
1. Тремя точками, не лежащими на одной прямой (рис.6.1).
2. Прямой и точкой, не лежащей на этой прямой (рис.6.2).
3. Двумя пересекающимися прямыми (рис.6.3).
4. Двумя параллельными прямыми (рис.6.4).
5. Любой плоской кривой или ломаной линией (например, треугольником) (рис.6.5).
Анализируя изображения на рис.6.1 – 6.5, можно заметить, что все изображения взаимосвязаны, и их можно заменять друг другом. Например, задание плоскости прямой и точкой можно получить из изображения плоскости тремя точками, соединив две из них прямой линией.
На плоскости (или в плоскости) можно построить точки и линии, принадлежащие этой плоскости. Для того, чтобы построить прямую, лежащую в плоскости, необходимо ее провести через две точки, лежащие в этой плоскости. В свою очередь, для построения точки, лежащей в плоскости, необходимо, чтобы она принадлежала линии, лежащей в этой плоскости. Например, прямая a принадлежит плоскости Γ, заданной треугольником ABC, т.к. она проведена через две точки A и 1, принадлежащие плоскости Γ (рис.6.6). Точка D принадлежит плоскости Γ, заданной треугольником ABC, т.к. она принадлежит прямой a, лежащей в плоскости Γ (рис.6.7). Вышесказанное носит название принципа принадлежности.
В любой плоскости можно провести фронталь и горизонталь, принадлежащие данной плоскости. Все фронтали одной и той же плоскости параллельны друг другу. Аналогично, все горизонтали одной и той же плоскости также параллельны друг другу (рис.6.8).
Кроме линий уровня в плоскости можно провести линии ската. Прямая ската t перпендикулярна горизонтали плоскости и этот угол проецируется в натуральную величину на горизонтальной плоскости проекций согласно теореме о проецировании прямого угла (рис.6.9). Прямая ската составляет максимальный угол с горизонтальной плоскостью проекций. Именно этим углом измеряется угол наклона данной плоскости к горизонтальной плоскости проекций. То же самое относится и к прямым линиям, лежащим в плоскости и перпендикулярным к фронтали. Такие прямые линии называются прямыми наибольшего угла наклона к фронтальной плоскости проекций.
На плоскости (или в плоскости) можно построить точки и линии, принадлежащие этой плоскости. Для того, чтобы построить прямую, лежащую в плоскости, необходимо ее провести через две точки, лежащие в этой плоскости. В свою очередь, для построения точки, лежащей в плоскости, необходимо, чтобы она принадлежала линии, лежащей в этой плоскости. Например, прямая a принадлежит плоскости Γ, заданной треугольником ABC, т.к. она проведена через две точки A и 1, принадлежащие плоскости Γ (рис.6.6). Точка D принадлежит плоскости Γ, заданной треугольником ABC, т.к. она принадлежит прямой a, лежащей в плоскости Γ (рис.6.7). Вышесказанное носит название принципа принадлежности.
В любой плоскости можно провести фронталь и горизонталь, принадлежащие данной плоскости. Все фронтали одной и той же плоскости параллельны друг другу. Аналогично, все горизонтали одной и той же плоскости также параллельны друг другу (рис.6.8).
Кроме линий уровня в плоскости можно провести линии ската. Прямая ската t перпендикулярна горизонтали плоскости и этот угол проецируется в натуральную величину на горизонтальной плоскости проекций согласно теореме о проецировании прямого угла (рис.6.9). Прямая ската составляет максимальный угол с горизонтальной плоскостью проекций. Именно этим углом измеряется угол наклона данной плоскости к горизонтальной плоскости проекций. То же самое относится и к прямым линиям, лежащим в плоскости и перпендикулярным к фронтали. Такие прямые линии называются прямыми наибольшего угла наклона к фронтальной плоскости проекций.





Плоскости могут занимать в пространстве общее и частное положение относительно плоскостей проекций. Ниже перечисляются возможные частные положения плоскостей.
1. Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально проецирующей (рис.6.10).
2. Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей (рис.6.11).
3. Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью уровня (рис.6.12).
4. Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью уровня (рис.6.13).
Плоскости уровня одновременно являются и проецирующими плоскостями. Плоскости частного положения можно задавать вышеперечисленными способами, а также, так называемой, вырожденной проекцией. Одна из проекций плоскости частного положения вырождается в прямую линию на той плоскости проекций, по отношению к которой она занимает проецирующее положение. Вторая проекция занимает всю область на второй плоскости проекций, как обычно, но ее не показывают (рис.6.10-6.13).
1. Плоскость, перпендикулярная фронтальной плоскости проекций, называется фронтально проецирующей (рис.6.10).
2. Плоскость, перпендикулярная горизонтальной плоскости проекций, называется горизонтально проецирующей (рис.6.11).
3. Плоскость, параллельная горизонтальной плоскости проекций, называется горизонтальной плоскостью уровня (рис.6.12).
4. Плоскость, параллельная фронтальной плоскости проекций, называется фронтальной плоскостью уровня (рис.6.13).
Плоскости уровня одновременно являются и проецирующими плоскостями. Плоскости частного положения можно задавать вышеперечисленными способами, а также, так называемой, вырожденной проекцией. Одна из проекций плоскости частного положения вырождается в прямую линию на той плоскости проекций, по отношению к которой она занимает проецирующее положение. Вторая проекция занимает всю область на второй плоскости проекций, как обычно, но ее не показывают (рис.6.10-6.13).





Прямые уровня и прямые ската проецирующих плоскостей и плоскостей уровня претерпевают некоторые изменения. На рис.6.14-6.17 заданы те же плоскости, что на рис.6.10-6.13, но с помощью пересекающихся прямых, в роли которых выступают фронтали и горизонтали. Для фронтально проецирующей плоскости ее горизонталь превращается в фронтально проецирующую прямую, а фронтальная проекция фронтали совпадает с вырожденной проекцией плоскости. Для горизонтально проецирующей плоскости ее фронталь превращается в горизонтально проецирующую прямую, а горизонтальная проекция горизонтали совпадает с вырожденной проекцией плоскости. Для горизонтальной плоскости уровня горизонтальная проекция горизонтали может располагаться, как угодно, а фронтальная проекция горизонтали совпадает с вырожденной проекцией плоскости, фронталь при этом превращается в профильно проецирующую прямую. Для фронтальной плоскости уровня фронтальная проекция фронтали может располагаться, как угодно, а горизонтальная проекция фронтали совпадает с вырожденной проекцией плоскости, горизонталь при этом превращается в профильно проецирующую прямую.
Для проецирующих плоскостей линиями ската являются сами фронтали и горизонтали, т.к. они перпендикулярны друг другу. Для плоскостей уровня одна из линий ската может быть любой прямой, лежащей в плоскости, а вторая превращается в проецирующую прямую.
Для проецирующих плоскостей линиями ската являются сами фронтали и горизонтали, т.к. они перпендикулярны друг другу. Для плоскостей уровня одна из линий ската может быть любой прямой, лежащей в плоскости, а вторая превращается в проецирующую прямую.
7. ЗАДАНИЕ ПОВЕРХНОСТЕЙ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ. ОБЩИЕ ПОЛОЖЕНИЯ
7.1. Линейчатые развертывающиеся поверхности
Линейчатые развертывающиеся поверхности образуются непрерывным поступательным движением прямой линии, пересекающей другую наперед заданную линию. Таким образом, образующая этих поверхностей l i – прямая линия. Эти поверхности можно развернуть на плоскости. К ним относятся: цилиндрическая поверхность, призматическая поверхность, коническая поверхность, пирамидальная поверхность.
7.1.1. Цилиндрическая поверхность
Цилиндрическая поверхность Φ образуется движением образующей l i таким образом, чтобы образующая l i была параллельна некоему направлению n (l i || n) и пересекала кривую линию m (l i × m).
Линия n называется направлением образующей, а линия m – направляющей. Задание линий n и m достаточно для задания поверхности Φ. Таким образом, линии n и m являются элементами определителя цилиндрической поверхности Φ.
На рис.7.1а задана цилиндрическая поверхность с помощью определителя Φ(n, m). Следуя закону образования цилиндрической поверхности l i || n и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.1б задана цилиндрическая поверхность с помощью линейного каркаса образующих. На рис.7.1в представлен отсек цилиндрической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих, самой направляющей m и линией a.
Ниже приведено описание цилиндрической поверхности Φ в табличной форме.
Линия n называется направлением образующей, а линия m – направляющей. Задание линий n и m достаточно для задания поверхности Φ. Таким образом, линии n и m являются элементами определителя цилиндрической поверхности Φ.
На рис.7.1а задана цилиндрическая поверхность с помощью определителя Φ(n, m). Следуя закону образования цилиндрической поверхности l i || n и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.1б задана цилиндрическая поверхность с помощью линейного каркаса образующих. На рис.7.1в представлен отсек цилиндрической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих, самой направляющей m и линией a.
Ниже приведено описание цилиндрической поверхности Φ в табличной форме.
На рис. 7.1б построены также точки A и B. Точка A принадлежит поверхности Φ, т.к. она принадлежит линии, лежащей на этой поверхности (в данном случае образующей). Точка B не принадлежит этой поверхности, т.к. ее горизонтальная и фронтальная проекции не принадлежат проекциям одной и той же образующей, а лишь конкурируют с точками разных образующих. Линия a (часть линии обреза) принадлежит поверхности Φ, т.к. каждая ее точка принадлежит какой-либо образующей поверхности. Для цилиндрической поверхности (как и для всех линейчатых поверхностей) удобно в роли посредников при построении точек и линий, принадлежащих поверхности, использовать образующие.
Цилиндрическая поверхность (так же, как линия и плоскость) может занимать проецирующее положение. При этом все ее образующие перпендикулярны соответствующей плоскости проекций.
Цилиндрическая поверхность (так же, как линия и плоскость) может занимать проецирующее положение. При этом все ее образующие перпендикулярны соответствующей плоскости проекций.
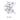


7.1.2. Призматическая поверхность
Призматическая поверхность Φ образуется движением образующей l i таким образом, чтобы образующая l i была параллельна некоему направлению n (l i || n) и пересекала ломаную линию m (l i × m). Линия n называется направлением образующей, а линия m – направляющей. Задание линий n и m достаточно для задания поверхности Φ. Таким образом, линии n и m являются элементами определителя призматической поверхности Φ.
На рис.7.2а задана призматическая поверхность с помощью определителя Φ (n, m). Следуя закону образования призматической поверхности l i || n и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.2б задана призматическая поверхность с помощью линейного каркаса образующих. На рис.7.2в представлен отсек призматической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих, самой направляющей m и линии a.
Ниже приведено описание призматической поверхности Φ в табличной форме.
На рис.7.2а задана призматическая поверхность с помощью определителя Φ (n, m). Следуя закону образования призматической поверхности l i || n и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.2б задана призматическая поверхность с помощью линейного каркаса образующих. На рис.7.2в представлен отсек призматической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих, самой направляющей m и линии a.
Ниже приведено описание призматической поверхности Φ в табличной форме.
Как видно из вышесказанного, призматическая поверхность очень похожа на цилиндрическую поверхность. Разница заключается лишь в форме направляющей. Призматическая поверхность так же, как цилиндрическая может занимать проецирующее положение.
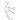



7.1.3. Коническая поверхность
Коническая поверхность Φ образуется движением образующей l i таким образом, чтобы образующая l i включала в себя некоторую точку S (l i כ S) и пересекала кривую линию m (l i × m). Точка S называется вершиной, а линия m – направляющей. Задание точки S и линии m достаточно для задания поверхности Φ. Таким образом, вершина S и направляющая m являются элементами определителя конической поверхности Φ.
На рис.7.3а задана коническая поверхность с помощью определителя Φ(S, m). Следуя закону образования конической поверхности l i כ S и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.3б задана коническая поверхность с помощью линейного каркаса образующих. На рис.7.3в представлен отсек конической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих и самой направляющей m. Ниже приведено описание конической поверхности Φ в табличной форме.
На рис.7.3а задана коническая поверхность с помощью определителя Φ(S, m). Следуя закону образования конической поверхности l i כ S и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.3б задана коническая поверхность с помощью линейного каркаса образующих. На рис.7.3в представлен отсек конической поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отсек ограничен линией обреза, состоящей из двух крайних образующих и самой направляющей m. Ниже приведено описание конической поверхности Φ в табличной форме.
Коническая поверхность похожа на цилиндрическую поверхность формой направляющей и отличается законом образования.




7.1.4. Пирамидальная поверхность
Пирамидальная поверхность Φ образуется движением образующей l i таким образом, чтобы образующая l i включала в себя некоторую точку S (l i כ S) и пересекала ломаную линию m (l i × m). Точка S называется вершиной, а линия m – направляющей. Задание точки S и линии m достаточно для задания поверхности Φ. Таким образом, вершина S и направляющая m являются элементами определителя пирамидальной поверхности Φ.
На рис.7.4а задана пирамидальная поверхность с помощью определителя Φ(S, m). Следуя закону образования пирамидальной поверхности l i כ S и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.4б задана пирамидальная поверхность с помощью линейного каркаса образующих. На рис.7.4в представлен отсек пирамидальной поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отек ограничен линией обреза, состоящей из двух крайних образующих и самой направляющей m. Ниже приведено описание пирамидальной поверхности Φ в табличной форме.
На рис.7.4а задана пирамидальная поверхность с помощью определителя Φ(S, m). Следуя закону образования пирамидальной поверхности l i כ S и l i × m, можно построить последовательный ряд образующих – каркас образующих. На рис.7.4б задана пирамидальная поверхность с помощью линейного каркаса образующих. На рис.7.4в представлен отсек пирамидальной поверхности, вырезанный из поверхности, заданной линейным каркасом образующих. Отек ограничен линией обреза, состоящей из двух крайних образующих и самой направляющей m. Ниже приведено описание пирамидальной поверхности Φ в табличной форме.
Пирамидальная поверхность похожа на коническую поверхность законом образования и отличается от нее формой образующей. В то же время она похожа на призматическую поверхность формой направляющей.

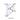


7.2. Поверхности вращения
Поверхности вращения образуются непрерывным вращательным движением образующей вокруг прямой линии i, называемой осью вращения. Поверхность вращения проще всего описать при проецирующем положении оси вращения. Невозможно перечислить все поверхности вращения как в предыдущем случае, т.к. любая новая форма образующей позволяет получить новую поверхность вращения. Ниже рассматриваются поверхность вращения общего вида, а также поверхности вращения, образованные вращением прямой линии и дуги окружности как наиболее часто используемые.
7.2.1. Поверхность вращения общего вида
На рис.7.5а представлена поверхность вращения общего вида, заданная определителем. Определитель и закон образования поверхности вращения всегда одинаков. Разница между поверхностями заключается лишь в форме образующей l i и ее положении относительно оси вращения i.
Ниже приведено описание поверхности вращения общего вида Φ в табличной форме.
Ниже приведено описание поверхности вращения общего вида Φ в табличной форме.
В отличие от линейчатых поверхностей для поверхностей вращения не всегда легко построить каркас образующих. В то же время при вращении каждая точка образующей описывает окружность радиусом, равным расстоянию от этой точки до оси (рис.7.5б). Эти окружности проецируются в натуральную величину на ту плоскость проекций, по отношению к которой ось вращения занимает проецирующее положение. На другую плоскость проекций они проецируются в виде горизонтальных прямых линий. Таким образом, они являются линиями уровня. Для поверхностей вращения эти линии называются параллелями (аналогично параллелям глобуса). Если продолжить аналогию с земным шаром, то образующие поверхности вращения можно назвать меридианами, а параллель с максимальным радиусом – экватором. На плоскости проекций, по отношению к которой ось вращения i занимает проецирующее положение, экватор является контуром проекции поверхности вращения. Параллель с минимальным радиусом называется горлом. Меридиан, который проецируется в натуральную величину в виде контура поверхности, называется главным меридианом. Таким образом, на поверхности вращения можно построить два семейства линий: параллели и меридианы. Т.е. каркас поверхности вращения может быть построен из параллелей или меридианов. Параллели строить проще, поэтому именно они используются для построения каркаса линий, с помощью которых можно строить точки, принадлежащие поверхности вращения (например, точка M).
При вращении прямой линии вокруг оси в зависимости от их взаимного положения образуются следующие поверхности: коническая поверхность вращения, цилиндрическая поверхность вращения, однополостный гиперболоид вращения.
При вращении прямой линии вокруг оси в зависимости от их взаимного положения образуются следующие поверхности: коническая поверхность вращения, цилиндрическая поверхность вращения, однополостный гиперболоид вращения.



7.2.2. Цилиндрическая поверхность вращения
Образующая цилиндрической поверхности вращения – прямая линия, параллельная оси вращения (рис.7.6). Цилиндрическую и коническую поверхности вращения можно также отнести одновременно и к классу линейчатых развертывающихся поверхностей. Однако поверхность принято относить к тому классу поверхностей, в котором их закон образования проще.


7.2.3.Коническая поверхность вращения
Образующая конической поверхности вращения – прямая линия, пересекающая ось вращения (рис.7.7). Линиями, удобными для построения, являются как параллели, так и меридианы, т.к. последние являются прямыми. Единственный случай, когда образующую конической поверхности вращения нельзя использовать для построения, это когда она является профильной прямой.
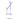

7.2.4.Однополостный гиперболоид вращения
Образующая однополостного гиперболоида вращения – прямая линия, скрещивающаяся с осью вращения (рис.7.8). Через каждую точку на поверхности гиперболоида вращения можно провести две образующие, которые будут касаться горла поверхности. Однако несмотря на то, что образующая является прямой линией, удобными для построения являются параллели. Построив каркас параллелей, можно построить контур поверхности. Меридианы гиперболоида вращения являются гиперболами.
Для построения контура (или очерка) гиперболоида вращения необходимо на заданной образующей взять ряд точек, начертить параллели, проходящие через эти точки. Тогда крайняя левая и правая точки этих параллелей на фронтальной плоскости проекций будут лежать на контуре фронтальной проекции. Самая близкая к оси точка будет вращаться с минимальным радиусом и образует при вращении горло поверхности. Для построения образующей, проходящей через заданную точку, необходимо через нее провести прямую, касающуюся горла. Таких прямых на горизонтальной плоскости проекций можно провести две, а затем по принадлежности перенести на фронтальную плоскость.
Для построения контура (или очерка) гиперболоида вращения необходимо на заданной образующей взять ряд точек, начертить параллели, проходящие через эти точки. Тогда крайняя левая и правая точки этих параллелей на фронтальной плоскости проекций будут лежать на контуре фронтальной проекции. Самая близкая к оси точка будет вращаться с минимальным радиусом и образует при вращении горло поверхности. Для построения образующей, проходящей через заданную точку, необходимо через нее провести прямую, касающуюся горла. Таких прямых на горизонтальной плоскости проекций можно провести две, а затем по принадлежности перенести на фронтальную плоскость.


7.2.5.Сферическая поверхность
7.2.6.Торовые поверхности
7.2.7.Кольцо
7.3. Каналовые и циклические поверхности
Каналовые поверхности подразделяются на каналовые поверхности с плоскостью параллелизма и нормальные каналовые поверхности. В первом случае поверхность образуется движением замкнутого контура вдоль направляющей параллельно какой-либо плоскости, называемой плоскостью параллелизма. Во втором случае плоский контур движется вдоль направляющей, при этом плоскость контура всегда перпендикулярна направляющей. Площади этих контуров в процессе перемещения могут монотонно изменяться.
Циклические поверхности могут рассматриваться как частный случай каналовых поверхностей, когда плоский контур является окружностью. На рис.7.13 представлена циклическая поверхность с плоскостью параллелизма, заданная определителем и каркасом образующих. В роли плоскости параллелизма в данном случае выступает горизонтальная плоскость проекций Π1. Ниже в табличной форме описана эта поверхность.


7.4. Линейчатые поверхности с плоскостью параллелизма
Линейчатые развертывающиеся поверхности образуются непрерывным движением прямой линии, которая при этом пересекает две направляющие и всегда параллельна какой-либо плоскости, называемой плоскостью параллелизма. К этому классу поверхностей относятся: гиперболический параболоид, коноид и цилиндроид. Определитель и закон образования всех поверхностей этого класса выглядит одинаково. Разница между ними заключается лишь в форме направляющих.
Построение каркаса образующих начинают с той плоскости проекций, по отношению к которой задана проецирующая плоскость параллелизма. В роли плоскости параллелизма может выступать одна из плоскостей проекций.
Построение каркаса образующих начинают с той плоскости проекций, по отношению к которой задана проецирующая плоскость параллелизма. В роли плоскости параллелизма может выступать одна из плоскостей проекций.

7.4.1. Гиперболический параболоид
7.4.2. Коноид
7.4.3. Цилиндроид
7.5. Винтовые поверхности (геликоиды)
Винтовые поверхности, или геликоиды, образуются непрерывным движением прямой линии, пересекающей винтовую линию. Остальные условия закона образования поверхности могут быть различны и в зависимости от этого образуются различные виды винтовых поверхностей. Ниже рассматриваются следующие винтовые поверхности: прямой геликоид, наклонный геликоид, конволютный геликоид.
7.5.1. Прямой геликоид
Прямой геликоид образуется непрерывным движением прямой линии, пересекающей две направляющие. В роли первой направляющей выступает винтовая линия, в роли второй – ось винтовой линии. При этом образующая должна быть параллельна плоскости, которая перпендикулярна оси винтовой линии (рис.7.17). Этот геликоид можно также отнести и к коноидам, т.к. одна его направляющая – кривая, а вторая – прямая. Плоскостью параллелизма для прямого геликоида, представленного на рис.7.17, является горизонтальная плоскость проекций Π1.
Ниже в табличной форме описана эта поверхность.
Ниже в табличной форме описана эта поверхность.




7.5.2. Наклонный геликоид
Наклонный геликоид образуется непрерывным движением прямой линии, пересекающей две направляющие. В роли первой направляющей выступает винтовая линия, в роли второй – ось винтовой линии. При этом образующая должна быть параллельна соответствующей образующей конуса вращения, мысленно представленного и совмещенного своей осью с осью винтовой линии (рис.7.18). Т.е. угол наклона образующих геликоида к оси равен углу наклона соответствующей образующей конуса к своей оси вращения. Этот конус называется конусом параллелизма.
Ниже в табличной форме описана эта поверхность.
Ниже в табличной форме описана эта поверхность.




7.5.3. Конволютный геликоид
Конволютный геликоид образуется непрерывным движением прямой линии, пересекающей винтовую линию, касающейся цилиндрической поверхности вращения и параллельной плоскости параллелизма. Плоскостью параллелизма для конволютного геликоида, представленного на рис.7.19, является горизонтальная плоскость проекций Π1. Конволютный геликоид задан отсеком, ограниченным винтовой линией m и винтовой линией a (рис.7.19в). Этот геликоид также можно отнести к цилиндроидам, т.к. его образующие пересекают две кривые (винтовые) линии и параллельны плоскости параллелизма. Конволютный геликоид является, так называемым, открытым геликоидом.
Ниже в табличной форме описана эта поверхность.
Ниже в табличной форме описана эта поверхность.




8. ПОЗИЦИОННЫЕ ЗАДАЧИ. ОБЩИЕ ПОЛОЖЕНИЯ
Задачи о взаимном расположении геометрических образов называются позиционными. Если геометрические образы располагаются достаточно близко друг к другу, то они могут пересекаться. В случае пересечения поверхности и линии результатом пересечения является точка (или точки) и такая задача называется первой главной позиционной задачей (IГПЗ). При пересечении двух поверхностей результатом пересечения является линия (или линии) и такая задача называется второй главной позиционной задачей (IIГПЗ). В свою очередь, при решении каждой из двух главных позиционных задач возможны три варианта:
Необходимо помнить о том, что проецирующее положение могут занимать только прямая линия, плоскость, цилиндрическая и призматическая поверхности.
- Оба пересекающихся геометрических образа занимают проецирующее положение;
- Один из пересекающихся геометрических образов занимает проецирующее положение;
- Ни один из пересекающихся геометрических образов не занимает проецирующего положения.
Необходимо помнить о том, что проецирующее положение могут занимать только прямая линия, плоскость, цилиндрическая и призматическая поверхности.
8.1. Первая и вторая главные позиционные задачи (вариант 1)
При пересечении двух проецирующих геометрических образов решение уже имеется на комплексном чертеже и его необходимо лишь обозначить.




При пересечении прямой a и плоскости Γ, занимающих проецирующее положение (IГПЗ, вариант 1), результатом пересечения является точка K (рис.8.1). При пересечении прямой a и цилиндрической поверхности Δ, занимающих проецирующее положение (IГПЗ, вариант 1), результатом пересечения являются две точки K и K/ (рис.8.2).
В результате пересечения плоскости Γ и цилиндрической поверхности Φ, занимающих проецирующее положение (IIГПЗ, вариант 1), образуется линия пересечения m (рис.8.3). В результате пересечения двух цилиндрических поверхностей Γ и Φ, занимающих проецирующее положение (IIГПЗ, вариант 1), образуется линия пересечения m (рис.8.4).
Как видно из чертежей во всех рассмотренных выше примерах, решение уже имеется на комплексном чертеже, и оно совпадает на каждой из плоскостей проекций с тем геометрическим образом, который занимает проецирующее положение по отношению к этой плоскости проекций, одновременно принадлежа и другому геометрическому образу.
В результате пересечения плоскости Γ и цилиндрической поверхности Φ, занимающих проецирующее положение (IIГПЗ, вариант 1), образуется линия пересечения m (рис.8.3). В результате пересечения двух цилиндрических поверхностей Γ и Φ, занимающих проецирующее положение (IIГПЗ, вариант 1), образуется линия пересечения m (рис.8.4).
Как видно из чертежей во всех рассмотренных выше примерах, решение уже имеется на комплексном чертеже, и оно совпадает на каждой из плоскостей проекций с тем геометрическим образом, который занимает проецирующее положение по отношению к этой плоскости проекций, одновременно принадлежа и другому геометрическому образу.
8.2. Первая и вторая главные позиционные задачи (вариант 2)
Плоскость Γ перпендикулярна оси вращения конической поверхности. Линия пересечения a является окружностью (рис. 8.8а). Плоскость Γ образует с осью вращения конической поверхности угол, больший угла φ при вершине конуса. Линия пересечения a является эллипсом (рис. 8.8б). Плоскость Γ образует с осью вращения конической поверхности угол, равный углу φ при вершине конуса. Линия пересечения a является параболой (рис. 8.8в). Плоскость Γ образует с осью вращения конической поверхности угол, меньший угла φ при вершине конуса. Линия пересечения a является гиперболой, состоящей из двух ветвей (рис. 8.8г). Плоскость Γ проходит через вершину конической поверхности вращения и образует с осью угол, меньший угла φ при вершине конуса. Линиями пересечения являются две прямые a и a / — образующие конуса (рис. 8.8д). Плоскость Γ проходит через вершину конической поверхности вращения и образует с осью угол, равный углу φ при вершине. Линией пересечения является одна прямая a — образующая конуса (плоскость касается конуса по образующей) (рис. 8.8e). Плоскость Γ проходит через вершину конической поверхности вращения и образует с осью угол, больший угла при вершине. Линия пересечения a вырождается в точку, совпадающую с вершиной конуса S (рис. 8.8ж).










8.3. Первая главная позиционная задача (вариант 3)
При пересечении двух геометрических образов Γ и a, когда ни один из них не занимает проецирующего положения, решения нет ни на одной из плоскостей проекций. В этом случае необходимо прибегнуть к помощи дополнительного геометрического образа-посредника – поверхности Δ (в частном случае – плоскости), который должен включать в себя исходную линию a. Геометрический образ-посредник Δ при пересечении с исходной поверхностью Γ образует линию пересечения b, которая, находясь на поверхности Δ, пересечется с исходной линией a в каких-то точках, которые одновременно находятся и на поверхности Γ. Следовательно, эти точки являются точками пересечения исходной поверхности Γ и исходной линии a (рис.8.9а). Алгоритм решения первой главной позиционной задачи в общем случае, т.е. варианте 3, выглядит следующим образом:
- Вводится дополнительный геометрический посредник Δ כ a.
- Находится линия пересечения Δ × Γ = b.
- Находятся точки пересечения a × b = K.
- Определяется видимость линии a.
На рис.8.9б показано решение задачи о пересечении прямой a и сферической поверхности Γ на комплексном чертеже. Прямая a заключена в горизонтально проецирующую плоскость Δ, которая пересекается со сферической поверхностью по линии b, горизонтальная проекция b1 которой совпадает с вырожденной проекцией плоскости Δ1 и горизонтальной проекцией прямой a1. Фронтальная проекция линии b2 находится по принадлежности линии b сферической поверхности Γ, т.е. решается IIГПЗ в случае 2. Т.к. линия b и прямая a находятся в одной плоскости Δ, то они пересекутся в точках K и K/. На горизонтальной плоскости проекций положение точек K и K/ определяется по их принадлежности прямой a. Далее проводится анализ видимости прямой a. Между точками K и K/ на обеих плоскостях проекций прямая a не видна, т.к. сфера является замкнутой поверхностью. На фронтальной плоскости проекций за пределами точки K прямая видна, т.к. судя по ее положению на горизонтальной плоскости проекций, она находится на передней половине сферы. За пределами точки K/ на фронтальной плоскости проекций прямая не видна, т.к. судя по положению точки K/ на горизонтальной плоскости, она находится на задней половине сферы. На горизонтальной плоскости проекций за пределами точки K прямая a видна, т.к. судя по положению точки K на фронтальной плоскости проекций, она находится на верхней половине сферы. За пределами точки K/ прямая a не видна на горизонтальной плоскости проекций, т.к. судя по положению точки K/ на фронтальной плоскости, она находится на нижней половине сферы. Таким образом, сфера заслоняет на фронтальной плоскости проекций все, что находится на задней половине, а на горизонтальной плоскости проекций она заслоняет все, что находится на ее нижней половине, т.е. ниже экватора. В данной задаче прямая a заключалась в горизонтально проецирующую плоскость. Аналогичным образом прямую a можно было заключить и во фронтально проецирующую плоскость. Решение при этом осталось бы прежним. При пересечении винтовой линии a и сферической поверхности Γ (рис.8.10) винтовую линию возможно заключить лишь в цилиндрическую проецирующую поверхность Δ, которая в пересечении со сферой даст линию пересечения b, являющуюся окружностью. В пересечении линий a и b получаются точки K и K/.





При решении задачи о пересечении прямой линии и конической поверхности вращения (рис.8.11а) прямую a можно было бы заключить во фронтально проецирующую плоскость и тогда, в зависимости от положения прямой, линия b представляла собой либо эллипс, либо параболу, либо гиперболу. При заключении прямой a в горизонтально проецирующую плоскость линия b представляла бы собой гиперболу. Т.е. во всех случаях линия b – это лекальная кривая, которую необходимо строить по точкам и степень точности решения зависит от числа построенных точек на линии b. Такое решение в любом случае считается приближенным. Если прямую a заключить в плоскость таким образом, чтобы линия b являлась прямой линией, то решение можно было бы считать точным. Для конической поверхности это возможно, если прямую a заключить в плоскость, проходящую через вершину конуса S. Тогда линия b будет состоять из двух образующих конуса (рис.8.11б). Плоскость Δ в этом случае будет плоскостью общего положения. Эта плоскость Δ уже задана на чертеже прямой a и точкой S (Δ(a, S)). Остается найти линию пересечения b этой плоскости Δ с поверхностью конуса Γ. Для этого необходимо перейти от задания плоскости Δ прямой и точкой к заданию плоскости Δ двумя пересекающимися прямыми c и d (Δ(c×d)), проходящими через вершину S. Горизонтальные проекции прямых c и d, взятых на фронтальной плоскости совершенно произвольно, определяются через точки их пересечения 1 и 2 с прямой a. Эти прямые c и d пересекают проецирующую плоскость Σ, в которой находится основание конуса, в точках 3 и 4. Плоскость Δ(c×d) пересекает плоскость Σ по прямой h. Точки 5 и 6 являются точками пересечения плоскости Δ с контуром основания. Таким образом, зная, что плоскость Δ пересекает конус по образующим и имея по две точки на этих образующих (точки S и 5 и точки S и 6), можно построить эти образующие b и b/. Точки пересечения K и K/ прямой a с образующими b и b/ являются точками пересечения прямой a и поверхности конуса Γ. Аналогичным образом может быть решена задача и для любой конической поверхности, если ее основание (направляющая) находится в проецирующей плоскости. В случае пересечения прямой линии с цилиндрической поверхностью также можно получить точное решение путем введения дополнительной плоскости общего положения, заданной двумя параллельными прямыми. Эти прямые должны быть параллельны образующим цилиндрической поверхности. Итак, при решении первой главной позиционной задачи выбор дополнительного геометрического образа-посредника Δ необходимо осуществлять таким образом, чтобы линия его пересечения b с исходной поверхностью Γ была, по возможности, простой (линия считается простой, если ее можно построить с помощью циркуля и линейки) и решение можно было считать точным.
8.4. Вторая главная позиционная задача (вариант 3)
При пересечении двух поверхностей Γ и Φ, когда ни одна из них не занимает проецирующего положения, решения нет ни на одной из плоскостей проекций. Для достижения цели необходимо прибегнуть к помощи дополнительных геометрических образов-посредников. В роли посредников могут выступать поверхности Δ i, которые пересекают обе исходные поверхности по линиям a i и b i. Т.к. линии a i и b i находятся на одной и той же поверхности Δ i, то они возможно пересекутся между собой в каких-то точках K i. Точки K i будут принадлежать одновременно исходным поверхностям Γ и Φ, т.е. лежать на линии их пересечения k (рис.8.12а). Алгоритм решения второй главной позиционной задачи в общем случае, т.е. варианте 3, выглядит следующим образом:
- Вводится дополнительный геометрический посредник Δ i.
- Находятся линии пересечения Δ i × Γ = a i, Δ i × Φ = b i.
- Находятся точки пересечения a i × b i = K i.
- После неоднократного повторения вышеописанного процесса и накопления достаточного количества точек K i строится линия пересечения k как совокупность точек K i: ∑K i = k.
- Определяется видимость линии пересечения k и поверхностей Γ и Φ.
Геометрический образ-посредник Δ i выбирается таким образом, чтобы линии пересечения a i и b i получались простыми, т.е. их можно было бы построить с помощью циркуля и линейки. В каждой конкретной задаче этот выбор осуществляется в зависимости от того, какие геометрические образы пересекаются, и какое положение они занимают относительно плоскостей проекций. В настоящем курсе для решения второй главной позиционной задачи используются геометрические образы-посредники в виде плоскостей и в виде концентрических сфер. В первом случае используемый способ называется методом секущих плоскостей, а во втором – методом концентрических сфер. Независимо от того, какой метод используется, алгоритм решения второй главной позиционной задачи остается общим.
На рис.8.12б показано решение задачи о пересечении конической поверхности Γ со сферической поверхностью Φ методом секущих плоскостей. В роли дополнительного геометрического образа-посредника Δ i приняты горизонтальные плоскости уровня, которые пересекаются с конической поверхностью по окружностям a i, а со сферической поверхностью по окружностям b i. Эти окружности a i и b i на фронтальной плоскости проекций совпадают с вырожденной проекцией горизонтальной плоскости уровня Δ2 i. На горизонтальной плоскости проекций окружности a i и b i, лежащие в одной плоскости пересекаются в точках K1 i и K1 i/, которые лежат на линии пересечения k поверхностей Γ и Φ. Фронтальные проекции точек K2 и K2/ определяются по их принадлежности линиям a2 i и b2 i или плоскости уровня Δ2 i. Для накопления достаточного количества таких точек процесс повторяется неоднократно. При выборе секущих плоскостей Δ i необходимо провести плоскость, проходящую по экватору сферической поверхности, т.к. в точках, полученных в результате, будет происходить переход видимости на горизонтальной плоскости проекций. Далее определяется видимость линии пересечения k и контуров поверхностей Γ и Φ. Метод секущих плоскостей имеет более широкую область применения, чем метод концентрических сфер, использование которого ограничено некоторыми условиями. Метод концентрических сфер можно применять, если:
а) пересекаются две поверхности вращения;
б) оси вращения этих поверхностей пересекаются;
в) пересекающиеся оси вращения образуют плоскость, параллельную какой-либо плоскости проекций.
Несмотря на ограничения, метод концентрических сфер используется достаточно часто, т.к. в ряде случаев позволяет получать простые решения.
На рис.8.12б показано решение задачи о пересечении конической поверхности Γ со сферической поверхностью Φ методом секущих плоскостей. В роли дополнительного геометрического образа-посредника Δ i приняты горизонтальные плоскости уровня, которые пересекаются с конической поверхностью по окружностям a i, а со сферической поверхностью по окружностям b i. Эти окружности a i и b i на фронтальной плоскости проекций совпадают с вырожденной проекцией горизонтальной плоскости уровня Δ2 i. На горизонтальной плоскости проекций окружности a i и b i, лежащие в одной плоскости пересекаются в точках K1 i и K1 i/, которые лежат на линии пересечения k поверхностей Γ и Φ. Фронтальные проекции точек K2 и K2/ определяются по их принадлежности линиям a2 i и b2 i или плоскости уровня Δ2 i. Для накопления достаточного количества таких точек процесс повторяется неоднократно. При выборе секущих плоскостей Δ i необходимо провести плоскость, проходящую по экватору сферической поверхности, т.к. в точках, полученных в результате, будет происходить переход видимости на горизонтальной плоскости проекций. Далее определяется видимость линии пересечения k и контуров поверхностей Γ и Φ. Метод секущих плоскостей имеет более широкую область применения, чем метод концентрических сфер, использование которого ограничено некоторыми условиями. Метод концентрических сфер можно применять, если:
а) пересекаются две поверхности вращения;
б) оси вращения этих поверхностей пересекаются;
в) пересекающиеся оси вращения образуют плоскость, параллельную какой-либо плоскости проекций.
Несмотря на ограничения, метод концентрических сфер используется достаточно часто, т.к. в ряде случаев позволяет получать простые решения.





На рис.8.13а, б показано решение задачи о пересечении цилиндрической поверхности вращения Γ и конической поверхности вращения Φ. Задачу можно решать методом концентрических сфер, т.к. выполнены все три необходимых условия. Точки A, B, C и D находятся на линии пересечения поверхностей k, т.к. контурные образующие обеих поверхностей Γ и Φ лежат в одной плоскости и, следовательно, пересекаются. Центры сфер-посредников Δ i располагаются в точке пересечения O осей поверхностей вращения. При пересечении поверхности вращения с соосной ей сферой линия их пересечения является окружностью, которая на одной из плоскостей проекций проецируется в виде прямой. Выбор радиуса R сфер-посредников ограничен некоторым диапазоном, за пределами которого невозможно получить решение. Сферы, имеющие радиус R в пределах Rmin ≤ R ≤ Rmax, позволяют получить точки, лежащие на линии пересечения. Расстояние от центра сфер O до наиболее удаленной точки D дает максимальный радиус Rmax. Минимальный радиус Rmin равен наибольшему из радиусов R1 и R2 двух сфер, вписанных в каждую из поверхностей. Сфера Δ i пересекается с цилиндрической поверхностью Γ по окружности a i, а с конической поверхностью Φ – по окружности b i. Окружность a i пересекается с окружностью b i в точке K i, которая лежит на линии пересечения поверхностей. Проведя несколько таких сфер, можно получить достаточное количество точек K i для построения линии пересечения k поверхностей Γ и Φ.
В отличие от метода секущих плоскостей метод концентрических сфер позволяет получить решение полностью на одной из плоскостей проекций, а затем перенести его на вторую плоскость проекций по принадлежности линии пересечения одному из геометрических образов. В рассмотренной задаче это удобно сделать по принадлежности линии пересечения k конической поверхности Φ.
На рис.8.13б представлено решение задачи при других пропорциях конической и цилиндрической поверхностей.
При пересечении двух поверхностей вращения и выполнении вышеперечисленных условий для применения метода концентрических сфер, а также возможности вписать в эти поверхности общую сферу, ветви линий пересечения k превращаются в две плоские кривые, лежащие в проецирующих плоскостях. Это утверждение носит название теоремы Монжа (рис.8.13в). При этом ветви линии пересечения пересекаются между собой в точке пересечения линий касания касательной сферы с исходными поверхностями (точка M).
В отличие от метода секущих плоскостей метод концентрических сфер позволяет получить решение полностью на одной из плоскостей проекций, а затем перенести его на вторую плоскость проекций по принадлежности линии пересечения одному из геометрических образов. В рассмотренной задаче это удобно сделать по принадлежности линии пересечения k конической поверхности Φ.
На рис.8.13б представлено решение задачи при других пропорциях конической и цилиндрической поверхностей.
При пересечении двух поверхностей вращения и выполнении вышеперечисленных условий для применения метода концентрических сфер, а также возможности вписать в эти поверхности общую сферу, ветви линий пересечения k превращаются в две плоские кривые, лежащие в проецирующих плоскостях. Это утверждение носит название теоремы Монжа (рис.8.13в). При этом ветви линии пересечения пересекаются между собой в точке пересечения линий касания касательной сферы с исходными поверхностями (точка M).
9. МЕТРИЧЕСКИЕ ЗАДАЧИ
Задачи, в которых определяются натуральные величины отрезков, углов, а также натуральные формы плоских фигур, называются метрическими. Метрические задачи подразделяются на два типа.
Первая основная метрическая задача (1ОМЗ) – это задача о нахождении натуральной величины отрезка. Такая задача выше уже решалась методом прямоугольного треугольника (рис.4.5). Решение этой задачи возможно также методами преобразования комплексного чертежа (см. раздел 10).
Вторая основная метрическая задача (2ОМЗ) – это задача о построении прямой, перпендикулярной заданной плоскости (прямая задача), или, наоборот, о построении плоскости, перпендикулярной заданной прямой (обратная задача). В настоящем разделе описывается решение второй основной метрической задачи.
Известно, что прямая перпендикулярна плоскости, если она перпендикулярна каким-либо двум пересекающимся прямым, лежащим в этой плоскости. Если в роли этих пересекающихся прямых выступают любые фронталь и горизонталь этой плоскости, то прямой угол между прямой и соответствующими проекциями фронтали и горизонтали будет проецироваться в натуральную величину согласно теореме о проецировании прямого угла. Из этого вытекает условие перпендикулярности прямой и плоскости: прямая n перпендикулярна плоскости Γ, если ее фронтальная проекции n2 перпендикулярна фронтальной проекции f2 фронтали плоскости, а ее горизонтальная проекция n1 перпендикулярна горизонтальной проекции h1 горизонтали плоскости (n2 ┴ f2, n1 ┴ h1).
На рис.9.1 к плоскости, заданной ∆ABC, построен перпендикуляр n в точке A. На рис.9.2 показано построение плоскости Γ, перпендикулярной прямой a (плоскость задана фронталью f и горизонталью h).
Если плоскость является проецирующей, то прямая, перпендикулярная к ней, является прямой уровня и перпендикулярность сохраняется между вырожденной проекцией плоскости и соответствующей проекцией прямой (рис.9.3).
Первая основная метрическая задача (1ОМЗ) – это задача о нахождении натуральной величины отрезка. Такая задача выше уже решалась методом прямоугольного треугольника (рис.4.5). Решение этой задачи возможно также методами преобразования комплексного чертежа (см. раздел 10).
Вторая основная метрическая задача (2ОМЗ) – это задача о построении прямой, перпендикулярной заданной плоскости (прямая задача), или, наоборот, о построении плоскости, перпендикулярной заданной прямой (обратная задача). В настоящем разделе описывается решение второй основной метрической задачи.
Известно, что прямая перпендикулярна плоскости, если она перпендикулярна каким-либо двум пересекающимся прямым, лежащим в этой плоскости. Если в роли этих пересекающихся прямых выступают любые фронталь и горизонталь этой плоскости, то прямой угол между прямой и соответствующими проекциями фронтали и горизонтали будет проецироваться в натуральную величину согласно теореме о проецировании прямого угла. Из этого вытекает условие перпендикулярности прямой и плоскости: прямая n перпендикулярна плоскости Γ, если ее фронтальная проекции n2 перпендикулярна фронтальной проекции f2 фронтали плоскости, а ее горизонтальная проекция n1 перпендикулярна горизонтальной проекции h1 горизонтали плоскости (n2 ┴ f2, n1 ┴ h1).
На рис.9.1 к плоскости, заданной ∆ABC, построен перпендикуляр n в точке A. На рис.9.2 показано построение плоскости Γ, перпендикулярной прямой a (плоскость задана фронталью f и горизонталью h).
Если плоскость является проецирующей, то прямая, перпендикулярная к ней, является прямой уровня и перпендикулярность сохраняется между вырожденной проекцией плоскости и соответствующей проекцией прямой (рис.9.3).



Условие перпендикулярности двух плоскостей сводится к условию перпендикулярности прямой и плоскости и основывается на том, что плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости. Возможно и обратное утверждение: если две плоскости взаимно перпендикулярны, то каждая из них проходит через перпендикуляр к другой плоскости. На рис.9.4 показаны две плоскости, перпендикулярные друг к другу: плоскость, заданная ∆DEA, перпендикулярна плоскости ∆ABC, т.к. ∆DEA включает в себя прямую n, перпендикулярную ∆ABC.
Условие перпендикулярности двух прямых общего положения также сводится к условию перпендикулярности прямой и плоскости и основывается на том, что любая прямая b, лежащая в плоскости Γ(f × h), перпендикулярной заданной прямой a, и проходящая через точку пересечения K этой плоскости Γ с заданной прямой a, также перпендикулярна заданной прямой a (рис.9.5). Точка M взята на плоскости Γ произвольно для построения прямой b.
Задачи на определение расстояния от точки до плоскости, расстояния между двумя параллельными плоскостями, расстояния между параллельными прямыми линиями можно свести к комплексному решению с использованием задач о перпендикулярности прямой линии и плоскости, пересечении прямой линии и плоскости и определении натуральной величины отрезка. На рис.9.6 приведено решение задачи об определении расстояния от точки M до плоскости Γ (∆ABC).
Алгоритм решения этой задачи выглядит следующим образом:
Условие перпендикулярности двух прямых общего положения также сводится к условию перпендикулярности прямой и плоскости и основывается на том, что любая прямая b, лежащая в плоскости Γ(f × h), перпендикулярной заданной прямой a, и проходящая через точку пересечения K этой плоскости Γ с заданной прямой a, также перпендикулярна заданной прямой a (рис.9.5). Точка M взята на плоскости Γ произвольно для построения прямой b.
Задачи на определение расстояния от точки до плоскости, расстояния между двумя параллельными плоскостями, расстояния между параллельными прямыми линиями можно свести к комплексному решению с использованием задач о перпендикулярности прямой линии и плоскости, пересечении прямой линии и плоскости и определении натуральной величины отрезка. На рис.9.6 приведено решение задачи об определении расстояния от точки M до плоскости Γ (∆ABC).
Алгоритм решения этой задачи выглядит следующим образом:
- Из точки M опускается перпендикуляр на плоскость Γ (2ОМЗ), n ┴ Γ → n2 ┴ f2, n1 ┴ h1.
- Находится точка пересечения K перпендикуляра n с плоскостью Γ (IГПЗ), Γ × n = K → Δ כ n, Δ × Γ = b, n × b = K.
- Находится натуральная величина отрезка MK (1ОМЗ).


10. ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА. ОБЩИЕ ПОЛОЖЕНИЯ
Решение как позиционных, так и метрических задач значительно упрощается в случае, когда геометрические образы занимают проецирующее положение, либо какие-то элементы этих геометрических образов занимают удобное для решения положение (например, положение линии уровня). Методы, позволяющие получать решение задач при наиболее удобном положении геометрических образов, называются методами преобразования комплексного чертежа. В настоящем курсе рассматриваются три метода преобразования комплексного чертежа:
- Метод замены плоскостей проекций.
- Метод вращения вокруг проецирующей оси.
- Метод вращения вокруг прямой уровня.
- Превращение прямой общего положения в прямую уровня.
- Превращение прямой уровня в проецирующую прямую.
- Превращение плоскости общего положения в проецирующую плоскость.
- Превращение проецирующей плоскости в плоскость уровня.
10.1. Метод замены плоскостей проекций
Преобразование комплексного чертежа, выполняемое этим методом, основано на том, что при введении новой плоскости проекций Π3 расстояние от любой точки геометрического образа до незаменяемой плоскости проекций (например, Π1), остается неизменным и равным расстоянию от проекции этой точки на заменяемой плоскости Π2 до линии пересечения между плоскостями проекций x21 (рис.10.1). Это расстояние остается прежним и в новой системе плоскостей проекций Π1 - Π3.
На рис.10.1 изображен отрезок прямой AB общего положения. В предыдущих разделах настоящего курса не возникало необходимости изображать линию пересечения между плоскостями проекций x21. При использовании метода замены плоскостей проекций изображать ее обязательно, т.к. именно от нее измеряются все расстояния. Индексы, присутствующие в обозначении линии, соответствуют индексам плоскостей проекций, которые пересекаются по этой линии.
На рис.10.1 изображен отрезок прямой AB общего положения. В предыдущих разделах настоящего курса не возникало необходимости изображать линию пересечения между плоскостями проекций x21. При использовании метода замены плоскостей проекций изображать ее обязательно, т.к. именно от нее измеряются все расстояния. Индексы, присутствующие в обозначении линии, соответствуют индексам плоскостей проекций, которые пересекаются по этой линии.
Для решения первой основной задачи преобразования комплексного чертежа необходимо, чтобы одна из проекций прямой AB стала перпендикулярна линиям связи (или параллельна прямой x, что одно и то же). С этой целью проводится новая линия пересечения плоскостей проекций, например, x13, параллельная горизонтальной проекции отрезка. Проводятся новые линии связи от точек A1 и B1, перпендикулярные x13, и вдоль них откладываются от линии x13 те же расстояния, что на заменяемой плоскости проекций Π2 от линии x21 до точек A2 и B2 (рис.10.2). В новой системе плоскостей проекций отрезок AB является прямой уровня, а его проекция A3B3 на плоскость Π3 является натуральной величиной отрезка AB.
Для решения второй основной задачи преобразования комплексного чертежа необходимо, чтобы одна из проекций отрезка AB, являющегося прямой уровня, совпала с линией связи, а вторая проекция выродилась в точку. Поэтому новую линию пересечения плоскостей проекций x13 необходимо провести перпендикулярно той проекции прямой уровня, которая является натуральной величиной (в данном случае, A1B1) (рис.10.3). Следует отметить, что для получения проецирующей прямой из прямой общего положения необходимо решить сначала первую задачу и только потом вторую задачу преобразования комплексного чертежа (рис.10.4).
Для решения второй основной задачи преобразования комплексного чертежа необходимо, чтобы одна из проекций отрезка AB, являющегося прямой уровня, совпала с линией связи, а вторая проекция выродилась в точку. Поэтому новую линию пересечения плоскостей проекций x13 необходимо провести перпендикулярно той проекции прямой уровня, которая является натуральной величиной (в данном случае, A1B1) (рис.10.3). Следует отметить, что для получения проецирующей прямой из прямой общего положения необходимо решить сначала первую задачу и только потом вторую задачу преобразования комплексного чертежа (рис.10.4).



Для решения третьей основной задачи преобразования комплексного чертежа необходимо, чтобы одна из проекций плоскости выродилась в прямую линию. В проецирующей плоскости одна из прямых уровня превращается в проецирующую прямую, поэтому в плоскости Γ (∆ ABC ) (рис.10.5) проводится, например, горизонталь h и новая линия пересечения плоскостей проекций x13, перпендикулярная ей. В новой системе плоскостей Π1 - Π3 горизонталь h стала проецирующей прямой, а проекция плоскости Γ3 выродилась в прямую линию. Следовательно, плоскость Γ стала проецирующей по отношению к плоскости проекций Π3.
Для решения четвертой основной задачи преобразования комплексного чертежа необходимо, чтобы вырожденная проекция проецирующей плоскости Γ (∆ ABC ) была параллельна линии пересечения между плоскостями проекций x13 (рис.10.6). Поэтому новая линия пересечения x13 проводится параллельно вырожденной проекции плоскости. В новой системе плоскостей проекций Π1 - Π3 проекция ∆ ABC на плоскость Π3 является натуральной величиной, плоскость Γ – плоскостью уровня. Необходимо отметить, что для получения плоскости уровня из плоскости общего положения следует решить сначала третью и только потом четвертую задачу преобразования комплексного чертежа (рис.10.7).
Для решения четвертой основной задачи преобразования комплексного чертежа необходимо, чтобы вырожденная проекция проецирующей плоскости Γ (∆ ABC ) была параллельна линии пересечения между плоскостями проекций x13 (рис.10.6). Поэтому новая линия пересечения x13 проводится параллельно вырожденной проекции плоскости. В новой системе плоскостей проекций Π1 - Π3 проекция ∆ ABC на плоскость Π3 является натуральной величиной, плоскость Γ – плоскостью уровня. Необходимо отметить, что для получения плоскости уровня из плоскости общего положения следует решить сначала третью и только потом четвертую задачу преобразования комплексного чертежа (рис.10.7).




10.2. Метод вращения вокруг проецирующей оси
Преобразование комплексного чертежа, выполняемое этим методом, основано на том, что при вращении геометрического образа вокруг какой-либо оси, занимающей проецирующее положение, можно добиться такого его положения, при котором решение поставленной задачи (например, позиционной) значительно упрощается.
На рис.10.8 показан отрезок прямой общего положения AB, который вращением вокруг горизонтально проецирующей оси i доведен до положения прямой уровня (в данном случае, фронтали). Ось i проведена через точку B, которая при вращении остается неподвижной. Для определения нового положения отрезка AB достаточно построить положение точки A после поворота. На горизонтальной плоскости проекций траектория движения точки A1 проецируется в виде окружности радиусом, равным горизонтальной проекции отрезка A1B1, а на фронтальной плоскости проекций траектория движения точки A2 проецируется в виде горизонтальной прямой, т.к. вращение происходит в горизонтальной плоскости уровня. Новое положение точки A¯ после поворота достигается в тот момент, когда горизонтальная проекция A¯1B¯1 становится перпендикулярной линиям связи (рис.10.9). Фронтальная проекция точки A¯2 после поворота определяется по ее принадлежности горизонтальной плоскости уровня Σ, в которой происходит вращение, и соблюдению проекционной связи между точками A¯2 и A¯1. В приведенном выше примере была решена первая основная задача преобразования комплексного чертежа. В данном случае прямая общего положения была преобразована во фронталь.


Для решения второй основной задачи преобразования комплексного чертежа необходимо, чтобы проекция отрезка A2B2 совпала с линией связи, а вторая проекция A1B1 выродилась в точку (рис.10.10). Это возможно, если отрезок AB изначально занимает положение прямой уровня. Проецирующее положение оси j выбирается по отношению к фронтальной плоскости проекций, т.к. вырождение в точку для фронтали возможно на горизонтальной плоскости проекций. Новое положение точки A после поворота достигается в момент, когда точка A2 при вращении вокруг оси j окажется на линии связи, а проекция B¯ совпадет с линией связи. При движении точка A1 достигнет состояния, при котором она совпадет с точкой B1 и при этом соблюдается проекционная связь с точкой A¯2. Полученный результат свидетельствует о том, что отрезок A¯B¯занимает проецирующее положение.




Для решения третьей основной задачи преобразования комплексного чертежа необходимо повернуть плоскость общего положения до состояния, когда она занимает проецирующее положение относительно какой-либо плоскости проекций. При этом одна из прямых уровня этой плоскости должна превратиться в проецирующую прямую. Это условие принимается в качестве признака проецирующего положения плоскости. На рис.10.11 задана плоскость общего положения Γ (∆ABC). Через точку A проведена ось i, занимающая проецирующее положение относительно горизонтальной плоскости проекций. При вращении вокруг этой оси горизонтали плоскости h возможно достижение ее фронтально проецирующего положения. Для этого на горизонтали h взята точка 1 и повернута радиусом A111 до состояния, когда горизонталь h займет проецирующее положение. При этом каждая точка плоскости Γ (∆ABC) повернется вокруг оси i на тот же угол, что и горизонталь h. Конфигурация треугольника после поворота не изменится. Поэтому если определить положение точек B и C после поворота, то удастся определить положение плоскости Γ (∆ABC) после поворота. Расстояния от точки 1 до точек B и C останутся после поворота неизменными, т.е. B111=B¯11¯1 и C111=C¯11¯1. Вследствие этого возможно из точки 11 циркулем засечь расстояния B111 и C111 на траекториях движения точек B1 и C1. Соединение полученных точек B¯1 и C¯1 между собой и с неподвижной точкой A1 определяет положение треугольника A¯B¯C¯ после поворота на горизонтальной плоскости проекций. Зная, что на фронтальной плоскости проекций точки B2 и C2 осуществляют движение в горизонтальных плоскостях уровня и, соблюдая проекционную связь между точками B¯1 и B¯2, а также точками C¯1 и C¯2, можно получить фронтальные проекции точек B¯2 и C¯2. При соединении между собой вершин B¯2 и C¯2 и неподвижной вершины A2, обнаруживается, что все три точки лежат на одной прямой, т.е. плоскость треугольника A¯B¯C¯ стала фронтально проецирующей.
Для решения четвертой основной задачи преобразования комплексного чертежа на рис.10.12 рассмотрена фронтально проецирующая плоскость Γ, заданная треугольником ABC. Признаком превращения проецирующей плоскости в плоскость уровня является перпендикулярность ее вырожденной проекции линиям связи. Для достижения этой цели через точку A проведена фронтально проецирующая ось j. Точка A при повороте вокруг оси j остается неподвижной, а точки B и C после поворота займут на фронтальной плоскости проекций положение B¯2 и C¯2, соответствующее горизонтальному расположению вырожденной проекции плоскости. Горизонтальные проекции точек B¯1 и C¯1 получены из условия их движения во фронтальных плоскостях уровня и соблюдения проекционной связи. Полученная горизонтальная проекция треугольника A¯B¯C¯ является его натуральной величиной, т.к. плоскость, заданная треугольником ABC является плоскостью уровня.
_____________________
Метод замены плоскостей проекций и метод вращения вокруг проецирующей оси позволяют решить одни и те же задачи. При использовании метода замены плоскостей проекций геометрический образ остается неподвижным, перемещению подвергаются только плоскости проекций. В случае вращения вокруг проецирующей оси – наоборот: без изменения остаются плоскости проекций, а геометрический образ подвергается вращению. Первый метод позволяет получать простые решения без громоздких построений, но направление развития построений иногда трудно предвидеть, и они могут занимать значительное пространство чертежа. Метод вращения вокруг проецирующей оси является компактным, развитие построений не выходит далеко за рамки заданного комплексного чертежа. Однако построения могут накладываться друг на друга и затруднять чтение чертежа. Выбор метода осуществляется, исходя из условия конкретной задачи.
Для решения четвертой основной задачи преобразования комплексного чертежа на рис.10.12 рассмотрена фронтально проецирующая плоскость Γ, заданная треугольником ABC. Признаком превращения проецирующей плоскости в плоскость уровня является перпендикулярность ее вырожденной проекции линиям связи. Для достижения этой цели через точку A проведена фронтально проецирующая ось j. Точка A при повороте вокруг оси j остается неподвижной, а точки B и C после поворота займут на фронтальной плоскости проекций положение B¯2 и C¯2, соответствующее горизонтальному расположению вырожденной проекции плоскости. Горизонтальные проекции точек B¯1 и C¯1 получены из условия их движения во фронтальных плоскостях уровня и соблюдения проекционной связи. Полученная горизонтальная проекция треугольника A¯B¯C¯ является его натуральной величиной, т.к. плоскость, заданная треугольником ABC является плоскостью уровня.
_____________________
Метод замены плоскостей проекций и метод вращения вокруг проецирующей оси позволяют решить одни и те же задачи. При использовании метода замены плоскостей проекций геометрический образ остается неподвижным, перемещению подвергаются только плоскости проекций. В случае вращения вокруг проецирующей оси – наоборот: без изменения остаются плоскости проекций, а геометрический образ подвергается вращению. Первый метод позволяет получать простые решения без громоздких построений, но направление развития построений иногда трудно предвидеть, и они могут занимать значительное пространство чертежа. Метод вращения вокруг проецирующей оси является компактным, развитие построений не выходит далеко за рамки заданного комплексного чертежа. Однако построения могут накладываться друг на друга и затруднять чтение чертежа. Выбор метода осуществляется, исходя из условия конкретной задачи.
Многие позиционные и метрические задачи решаются значительно проще и точнее при предварительном использовании методов преобразования комплексного чертежа. На рис.10.13 приведено решение задачи об определении расстояния от точки до плоскости методом замены плоскостей проекций. Эта задача решалась в разделе 9 и требовала достаточно трудоемких построений. При использовании метода замены плоскостей проекций плоскость Γ (∆ ABC ) преобразуется в проецирующую плоскость. В новой системе плоскостей проекций Π1 - Π3 расстояние от точки M до проецирующей плоскости Γ будет измеряться отрезком MK, являющимся перпендикуляром из точки M к плоскости Γ. Как видно из чертежа, это решение значительно проще предыдущего.
10.3. Метод вращения вокруг прямой уровня
Метод вращения вокруг прямой уровня отличается от вышеописанных методов тем, что с его помощью невозможно решить все четыре основные задачи преобразования комплексного чертежа. Однако его преимуществом является возможность с помощью только одного преобразования превратить плоскость общего положения в плоскость уровня, что позволяет получить в натуральную величину все, что находится в этой плоскости.


На рис.10.14 изображена плоскость Γ, заданная треугольником ABC, одна из сторон которого BC является горизонталью h. При повороте вокруг горизонтали h плоскости треугольника его вершины B и C, находящиеся на неподвижной горизонтали h, также остаются неподвижными. Следовательно, для построения плоскости треугольника ABC после поворота достаточно найти положение точки A после поворота. Вращение точки A вокруг горизонтали h происходит в плоскости Σ, перпендикулярной этой горизонтали (рис.10.15). Эта плоскость Σ занимает горизонтально проецирующее положение, и ее вырожденная проекция Σ1 составляет прямой угол с горизонтальной проекцией h1 горизонтали. Центром вращения точки A является точка O, поэтому проекциями радиуса вращения являются отрезки O1A1 и O2A2. После поворота точка A окажется на проекции плоскости Σ1 на расстоянии от точки O1, равном натуральной величине радиуса вращения OA точки A, т.к. точка A и точка O окажутся в горизонтальной плоскости уровня, проходящей через горизонталь h. Способом прямоугольного треугольника определяется натуральная величина OA и откладывается от точки O1 в плоскости Σ. Полученная точка A¯1 будет являться положением точки A1 после поворота. Треугольник A¯1B1C1 лежит в плоскости уровня, проходящей через горизонталь h и, следовательно, является натуральной величиной треугольника ABC.
Аналогичным образом можно повернуть любую плоскость вокруг собственной горизонтали или фронтали до состояния плоскости уровня. На рис.10.16 изображен треугольник ABC, когда ни одна из его сторон не является прямой уровня. Для превращения плоскости ∆ABC в плоскость уровня его необходимо повернуть вокруг какой-либо собственной прямой уровня. Для этой цели через точку C проведена горизонталь h. Точка C, как лежащая на горизонтали, в процессе поворота остается неподвижной. Точка A вращается вокруг точки O. Радиус ее вращения определяется точно так же, как в предыдущей задаче. Для определения положения точки B после поворота нет необходимости определять натуральную величину ее радиуса вращения. Достаточно определить положение точки B¯1 путем пересечения продолжения отрезка O1/B1 с продолжением отрезка A¯111. Это возможно, потому что точка 1 неподвижна и находится на стороне AB.
Аналогичным образом можно повернуть любую плоскость вокруг собственной горизонтали или фронтали до состояния плоскости уровня. На рис.10.16 изображен треугольник ABC, когда ни одна из его сторон не является прямой уровня. Для превращения плоскости ∆ABC в плоскость уровня его необходимо повернуть вокруг какой-либо собственной прямой уровня. Для этой цели через точку C проведена горизонталь h. Точка C, как лежащая на горизонтали, в процессе поворота остается неподвижной. Точка A вращается вокруг точки O. Радиус ее вращения определяется точно так же, как в предыдущей задаче. Для определения положения точки B после поворота нет необходимости определять натуральную величину ее радиуса вращения. Достаточно определить положение точки B¯1 путем пересечения продолжения отрезка O1/B1 с продолжением отрезка A¯111. Это возможно, потому что точка 1 неподвижна и находится на стороне AB.

В некоторых задачах с использованием метода вращения вокруг прямой уровня можно обойтись без определения натуральных величин способом прямоугольного треугольника. Для этой цели можно использовать вторую прямую уровня. На рис.10.17 изображена плоскость Γ, заданная двумя пересекающимися прямыми a и b. Требуется определить натуральную величину угла между прямыми a и b. Этот угол можно увидеть в натуральную величину, если плоскость Γ станет плоскостью уровня. Для этого ее необходимо повернуть вокруг собственной прямой уровня, например, вокруг горизонтали h. Точки 1 и 2, лежащие одновременно на горизонтали h и прямых a и b соответственно, остаются при повороте неподвижными. Для построения плоскости Γ после поворота достаточно повернуть одну точку, например точку K. Для этого через точку K в плоскости Γ проведена фронталь f, которая пересекает горизонталь h в точке M. После поворота плоскости Γ точка M, как принадлежащая горизонтали h, останется неподвижной, а точка K будет осуществлять вращение в проецирующей плоскости Σ. Отрезок M2K2, как принадлежащий фронтали, является натуральной величиной отрезка MK, поэтому его можно засечь циркулем из точки M1 на горизонтальной плоскости проекций. Полученная точка пересечения дуги радиуса MK с проекцией плоскости Σ1 дает положение точки K1 после поворота. Таким образом, полученная точка K¯1 позволяет построить положение фронтали f после поворота, а также положение прямых a и b после поворота. Полученная плоскость Γ¯(a¯× b¯) является плоскостью уровня, а угол между прямыми a¯1 и b¯1 является натуральной величиной угла между прямыми a и b.
Метод вращения вокруг прямой уровня компактен и наиболее удобен в случаях, когда геометрические образы находятся в одной плоскости и решение задач можно свести к задачам планиметрии.
Метод вращения вокруг прямой уровня компактен и наиболее удобен в случаях, когда геометрические образы находятся в одной плоскости и решение задач можно свести к задачам планиметрии.

11. КАСАТЕЛЬНАЯ ПЛОСКОСТЬ И НОРМАЛЬ К ПОВЕРХНОСТИ
Плоскость, касательная к поверхности в заданной точке, является геометрическим местом всех касательных прямых, проведенных к поверхности в этой точке. Для построения касательной плоскости достаточно построить хотя бы две касательные прямые в этой точке. Для этого необходимо построить на поверхности две какие-либо линии, проходящие через заданную точку. Тогда две касательные прямые линии к двум линиям, лежащим на поверхности, образуют касательную плоскость. Перпендикуляр, проведенный к касательной плоскости в точке касания, называется нормалью к поверхности в заданной точке. Построение такого перпендикуляра не представляет труда, если построена касательная плоскость. Достаточно провести в этой плоскости фронталь и горизонталь и выполнить условие перпендикулярности прямой и плоскости (вторая основная метрическая задача). Ниже рассматривается построение касательных плоскостей для различных поверхностей.
На рис.11.1 задана поверхность вращения общего вида. В точке M, лежащей на этой поверхности, необходимо построить касательную плоскость и нормаль. На поверхности вращения можно построить параллель и меридиан, проходящие через заданную точку M. Параллель в данном случае является горизонталью-окружностью, касательная к которой также является горизонталью h. Меридиан, проходящий через точку M, проецируется не в натуральную величину, и строить его достаточно трудоемкая задача. Поэтому воспользоваться этим меридианом как второй линией, к которой можно построить касательную прямую, будет сложно. Используя метод вращения вокруг проецирующей оси, точка M поворачивается вокруг оси i до совмещения с главным меридианом (с контурной образующей). В этом положении к точке M¯ можно построить касательную прямую t¯, т.к. главный меридиан на фронтальной плоскости проекций проецируется в натуральную величину. Все точки, лежащие на одной параллели, находятся по отношению к оси вращения i в одинаковом положении. Поэтому касательные прямые к меридианам, проходящим через все точки одной параллели, обязательно пересекут ось вращения i в одной и той же точке K и образуют конус касательных с вершиной в точке K. Плоскость, касательная к поверхности в точке M¯, является фронтально проецирующей, т.к. ее горизонталь h¯ выродилась в фронтально проецирующую прямую. Перпендикуляр к этой плоскости n¯ составит прямой угол с ее вырожденной проекцией Γ2, а его продолжение обязательно пересечет ось i в точке K2/. В этой же точке K2/ пересекут ось перпендикуляры к касательным плоскостям во всех точках, лежащих на одной параллели. Эти перпендикуляры образуют конус нормалей с вершиной в точке K/. Поэтому нормаль в точке M проходит через точку M и точку K/. Касательная плоскость Γ в точке M образована пересекающимися в этой точке прямыми h и t (h - прямая, касательная параллели и t - прямая, касательная меридиану).
На рис.11.1 задана поверхность вращения общего вида. В точке M, лежащей на этой поверхности, необходимо построить касательную плоскость и нормаль. На поверхности вращения можно построить параллель и меридиан, проходящие через заданную точку M. Параллель в данном случае является горизонталью-окружностью, касательная к которой также является горизонталью h. Меридиан, проходящий через точку M, проецируется не в натуральную величину, и строить его достаточно трудоемкая задача. Поэтому воспользоваться этим меридианом как второй линией, к которой можно построить касательную прямую, будет сложно. Используя метод вращения вокруг проецирующей оси, точка M поворачивается вокруг оси i до совмещения с главным меридианом (с контурной образующей). В этом положении к точке M¯ можно построить касательную прямую t¯, т.к. главный меридиан на фронтальной плоскости проекций проецируется в натуральную величину. Все точки, лежащие на одной параллели, находятся по отношению к оси вращения i в одинаковом положении. Поэтому касательные прямые к меридианам, проходящим через все точки одной параллели, обязательно пересекут ось вращения i в одной и той же точке K и образуют конус касательных с вершиной в точке K. Плоскость, касательная к поверхности в точке M¯, является фронтально проецирующей, т.к. ее горизонталь h¯ выродилась в фронтально проецирующую прямую. Перпендикуляр к этой плоскости n¯ составит прямой угол с ее вырожденной проекцией Γ2, а его продолжение обязательно пересечет ось i в точке K2/. В этой же точке K2/ пересекут ось перпендикуляры к касательным плоскостям во всех точках, лежащих на одной параллели. Эти перпендикуляры образуют конус нормалей с вершиной в точке K/. Поэтому нормаль в точке M проходит через точку M и точку K/. Касательная плоскость Γ в точке M образована пересекающимися в этой точке прямыми h и t (h - прямая, касательная параллели и t - прямая, касательная меридиану).

Для любой другой поверхности вращения справедливы аналогичные построения. Для сферической поверхности нормаль в любой точке на поверхности является продолжением ее радиуса, а касательная плоскость перпендикулярна радиусу сферы.
На рис.11.2 изображена коническая поверхность, к которой в точке M необходимо построить касательную плоскость Γ и нормаль n. Через точку M проведена окружность, принадлежащая конической поверхности. К этой окружности в точке M можно провести касательную прямую h, являющуюся горизонталью. Второй линией, к которой можно провести касательную прямую, является образующая конической поверхности l. Касательная к прямой линии совпадает с ней. Таким образом, прямая l является второй касательной. Касательная плоскость Γ образована двумя пересекающимися прямыми h и l. Для построения нормали n к поверхности Γ необходимо построить фронталь f касательной плоскости. Прямая n, удовлетворяющая условиям: n2 ┴ f2, n1 ┴ h1, является перпендикуляром к плоскости Γ и, следовательно, является нормалью к конической поверхности в точке M.
На рис.11.2 изображена коническая поверхность, к которой в точке M необходимо построить касательную плоскость Γ и нормаль n. Через точку M проведена окружность, принадлежащая конической поверхности. К этой окружности в точке M можно провести касательную прямую h, являющуюся горизонталью. Второй линией, к которой можно провести касательную прямую, является образующая конической поверхности l. Касательная к прямой линии совпадает с ней. Таким образом, прямая l является второй касательной. Касательная плоскость Γ образована двумя пересекающимися прямыми h и l. Для построения нормали n к поверхности Γ необходимо построить фронталь f касательной плоскости. Прямая n, удовлетворяющая условиям: n2 ┴ f2, n1 ┴ h1, является перпендикуляром к плоскости Γ и, следовательно, является нормалью к конической поверхности в точке M.
12. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ. ОБЩИЕ ПОЛОЖЕНИЯ
Поверхность называется развертывающейся, если она может быть совмещена с плоскостью без складок и разрывов. Плоская фигура, полученная в результате такого совмещения, называется разверткой поверхности. Точные развертки можно получить для следующих поверхностей: цилиндрических, призматических, конических, пирамидальных поверхностей, а также многогранников и некоторых геликоидов. Все остальные поверхности невозможно совместить с плоскостью без складок и разрывов. Однако с определенной степенью приближения их также можно развернуть. Далее рассматриваются свойства разверток и методы построения разверток только развертывающихся поверхностей.
12.1. Свойства разверток
Поверхности и их развертки обладают следующими свойствами:
- Каждой точке на поверхности соответствует точка на ее развертке, а также каждой точке на развертке соответствует точка на поверхности (рис.12.1).
- Длины двух линий на поверхности и на ее развертке равны между собой MK = M0K0 (рис.12.1).
- Замкнутая линия на поверхности и соответствующая ей линия на развертке ограничивают одинаковую площадь.
- Угол между двумя линиями на поверхности равен углу между соответствующими линиями на ее развертке (под углом между линиями подразумевается угол между касательными к линиям в точке пересечения).
- Прямой линии на поверхности соответствует прямая линия на ее развертке.
- Параллельным прямым на поверхности соответствуют параллельные прямые на развертке.
- Если отрезок линии на поверхности является отрезком прямой на развертке, то его длина является кратчайшим расстоянием между соответствующими точками на поверхности и такая линия называется геодезической.


12.2. Методы построения разверток
Для построения разверток используются следующие методы:
– метод треугольников (или метод триангуляции);
– метод раскатки;
– метод нормального сечения.
Часто используемым и имеющим наиболее широкую область применения является метод треугольников. Метод используется в тех случаях, когда поверхность легко разбивается на треугольники.
– метод треугольников (или метод триангуляции);
– метод раскатки;
– метод нормального сечения.
Часто используемым и имеющим наиболее широкую область применения является метод треугольников. Метод используется в тех случаях, когда поверхность легко разбивается на треугольники.
12.2.1. Метод треугольников
На рис.12.2 представлена шестигранная пирамида, основание которой лежит в горизонтальной плоскости уровня. Боковая поверхность этой пирамидальной поверхности представляет шесть различных треугольников, имеющих общие стороны (ребра).


Знание натуральной величины каждого ребра позволит построить эти треугольники. Пристраивая эти треугольники одинаковыми сторонами, можно получить развертку пирамидальной поверхности. Т.к. основание пирамиды находится в плоскости уровня, то стороны основания являются горизонталями и их натуральные величины имеются на горизонтальной плоскости проекций. Натуральные величины боковых ребер определяются методом прямоугольного треугольника. В отличие от традиционного использования этого метода в данной задаче в связи с тем, что разница по высоте (превышение S2O2) между вершиной S и точками основания одинакова, прямоугольный треугольник образуется путем пристраивания величины горизонтальных проекций боковых ребер к общему превышению S2O2 на фронтальной плоскости проекций. Такой подход позволяет избежать громоздких построений. На рис.12.2 изображена боковая поверхность шестигранной пирамиды.
Аналогичным образом можно построить развертку конической поверхности. Коническая поверхность заменяется вписанной в нее пирамидальной поверхностью. Для этого основание конической поверхности аппроксимируют ломаной линией. Чем большее число участков будет иметь ломаная, тем с большей точностью будет построена развертка конической поверхности.
В случае конической поверхности вращения ее развертка может быть построена точно, т.к. она является сектором круга радиуса l и центральным углом φ=360R/l=360l1/l2 где R – радиус основания конуса вращения, а l – длина образующей, или φ=360sinα, где α– угол при вершине конуса вращения (рис.12.3).
Аналогичным образом можно построить развертку конической поверхности. Коническая поверхность заменяется вписанной в нее пирамидальной поверхностью. Для этого основание конической поверхности аппроксимируют ломаной линией. Чем большее число участков будет иметь ломаная, тем с большей точностью будет построена развертка конической поверхности.
В случае конической поверхности вращения ее развертка может быть построена точно, т.к. она является сектором круга радиуса l и центральным углом φ=360R/l=360l1/l2 где R – радиус основания конуса вращения, а l – длина образующей, или φ=360sinα, где α– угол при вершине конуса вращения (рис.12.3).

Любая развертывающаяся поверхность может быть разбита на треугольники, поэтому метод треугольников применим ко всем развертывающимся поверхностям. Однако, в отдельных случаях, учитывая особенности поверхностей, можно использовать и другие методы.

12.2.2. Метод раскатки
На рис.12.4 представлена призматическая поверхность, боковые ребра которой являются горизонталями. Вращая вокруг каждого из боковых ребер грань призмы, проходящую через это ребро, можно получить натуральную величину этой грани.

Первоначально на рис.12.4 показано вращение ребра AA/ вокруг ребра CC/ . Положение точек A¯1 и A¯1/ после поворота определено из условия, что основание призмы лежит во фронтальной плоскости уровня, и отрезки AB, BC, AC на фронтальной плоскости проекций являются натуральными величинами. Далее ребро BB/ вращается вокруг ребра AA/, но результат вращения пристраивается не к отрезку A1A1/, а к отрезку A¯1A¯1/. Т.е. осуществляется параллельный перенос. Аналогично отрезок CC/ вращается вокруг ребра BB/, совмещая это с параллельным переносом. В результате трех последовательных вращений и параллельного переноса все грани призмы оказываются в натуральную величину и соединенными друг с другом, что позволяет считать полученную плоскую фигуру разверткой.
12.2.3. Метод нормального сечения
На рис.12.5 представлена цилиндрическая поверхность, образующие которой являются фронталями. Однако знание их натуральной величины не позволяет построить развертку. Для этой цели необходимо построить сечение этой поверхности плоскостью Δ, перпендикулярной образующим. Тогда натуральная длина полученной линии пересечения (нормального сечения), вытянутая на развертке в прямую линию, дает возможность отложить перпендикулярно ей отрезки, длины которых равны соответствующим участкам длин образующих. Натуральный вид нормального сечения определяется методом замены плоскостей проекций или вращением вокруг фронтали.


13. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ. ОБЩИЕ ПОЛОЖЕНИЯ
Несмотря на многочисленные преимущества комплексного чертежа, он обладает одним существенным недостатком: недостаточной наглядностью изображения. Большая степень наглядности может быть достигнута, если не стремиться располагать геометрический образ так, чтобы его какие-либо элементы занимали положение уровня или проецирующее положение относительно плоскостей проекций. В случаях, когда наглядность изображения является приоритетной, используют аксонометрические проекции. Ниже рассматривается механизм образования аксонометрического чертежа точки и его связь с комплексным чертежом.

На рис.13.1 изображена точка A и жестко связанная с ней декартова система координат OXYZ. Плоскость Π/ называется аксонометрической плоскостью проекций. Проекция декартовой системы координат на плоскость Π/ называется аксонометрической системой координат O/X/Y/Z/. Точка A/ называется аксонометрической проекцией точки A. Ломаная линия OAxA1A называется координатной ломаной, каждый отрезок которой соответствует декартовым координатам точки A. Соответствующая ломаная линия O/Ax/A1/A/ называется аксонометрической ломаной, каждый отрезок которой соответствует аксонометрическим координатам точки A.
Единицы измерения координат точек называются координатными масштабами. В декартовой системе координат этот масштаб e называется натуральным, а в аксонометрической системе координат – аксонометрическими масштабами ex/, ey/, ez/. В случае, когда направление проецирования перпендикулярно аксонометрической плоскости проекций, аксонометрия называется прямоугольной (или ортогональной). При этом аксонометрические масштабы будут меньше соответствующего натурального масштаба. Если направление проецирования не перпендикулярно аксонометрической плоскости проекций, то аксонометрия называется косоугольной, а аксонометрические масштабы могут быть даже больше соответствующего натурального.
Отношения величин аксонометрических масштабов к натуральному масштабу называются показателями искажения по соответствующим осям: по оси X/: u = e/x /e; по оси Y/: v = e/y /e; по оси Z/: w = e/z /e. В прямоугольной аксонометрии они меньше единицы, а в косоугольной могут быть и больше (но это не используется).
Показатели искажения могут быть разными по всем осям. В этом случае аксонометрия называется триметрией: u≠v≠w. Если показатели искажения равны по двум осям, то такая аксонометрия называется диметрией u=v≠w (или u=w≠v, или w=v≠u). Если все три показателя искажения равны u=v=w, то такая аксонометрия называется изометрией. Это справедливо как для ортогональной, так и для косоугольной аксонометрии.
Аксонометрические масштабы независимы друг от друга и могут выбираться произвольно. Это утверждение (принимаемое в настоящем курсе без доказательства) следует из теоремы Польке, которая гласит: всегда найдется такое положение прямоугольной системы натуральных координат в пространстве, такой натуральный масштаб и такое направление проецирования, при которых аксонометрическая система координат окажется параллельной проекцией натуральной системы.
Однако показатели искажения связаны между собой зависимостью:
u2 + v2 + w2 = 2 + ctgγ, где γ – угол наклона проецирующих лучей к аксонометрической плоскости проекций.
В случае ортогональной аксонометрии γ = 0, ctgγ = 0, u2 + v2 +w2 = 2. (1)
При дробных показателях искажения во избежание трудоемких вычислений один из них (максимальный) приравнивается к единице. Остальные показатели искажения пропорционально изменяются. Такие показатели искажения называются приведенными.
На рис.13.2 показано построение аксонометрического чертежа точки A по ее комплексному чертежу.
Единицы измерения координат точек называются координатными масштабами. В декартовой системе координат этот масштаб e называется натуральным, а в аксонометрической системе координат – аксонометрическими масштабами ex/, ey/, ez/. В случае, когда направление проецирования перпендикулярно аксонометрической плоскости проекций, аксонометрия называется прямоугольной (или ортогональной). При этом аксонометрические масштабы будут меньше соответствующего натурального масштаба. Если направление проецирования не перпендикулярно аксонометрической плоскости проекций, то аксонометрия называется косоугольной, а аксонометрические масштабы могут быть даже больше соответствующего натурального.
Отношения величин аксонометрических масштабов к натуральному масштабу называются показателями искажения по соответствующим осям: по оси X/: u = e/x /e; по оси Y/: v = e/y /e; по оси Z/: w = e/z /e. В прямоугольной аксонометрии они меньше единицы, а в косоугольной могут быть и больше (но это не используется).
Показатели искажения могут быть разными по всем осям. В этом случае аксонометрия называется триметрией: u≠v≠w. Если показатели искажения равны по двум осям, то такая аксонометрия называется диметрией u=v≠w (или u=w≠v, или w=v≠u). Если все три показателя искажения равны u=v=w, то такая аксонометрия называется изометрией. Это справедливо как для ортогональной, так и для косоугольной аксонометрии.
Аксонометрические масштабы независимы друг от друга и могут выбираться произвольно. Это утверждение (принимаемое в настоящем курсе без доказательства) следует из теоремы Польке, которая гласит: всегда найдется такое положение прямоугольной системы натуральных координат в пространстве, такой натуральный масштаб и такое направление проецирования, при которых аксонометрическая система координат окажется параллельной проекцией натуральной системы.
Однако показатели искажения связаны между собой зависимостью:
u2 + v2 + w2 = 2 + ctgγ, где γ – угол наклона проецирующих лучей к аксонометрической плоскости проекций.
В случае ортогональной аксонометрии γ = 0, ctgγ = 0, u2 + v2 +w2 = 2. (1)
При дробных показателях искажения во избежание трудоемких вычислений один из них (максимальный) приравнивается к единице. Остальные показатели искажения пропорционально изменяются. Такие показатели искажения называются приведенными.
На рис.13.2 показано построение аксонометрического чертежа точки A по ее комплексному чертежу.
На практике применяются различные виды аксонометрических изображений. В каждом конкретном случае выбор осуществляется, исходя из условия большей наглядности изображения и простоты построения. В ГОСТ (Государственный стандарт) рекомендуется применять следующие виды аксонометрии:
– прямоугольная изометрия;
– прямоугольная диметрия;
– косоугольная диметрия (кавальерная аксонометрия или кабинетная диметрия);
– косоугольная изометрия (военная аксонометрия).
В архитектурном проектировании могут применяться и другие виды аксонометрий, продиктованные композиционными соображениями.
– прямоугольная изометрия;
– прямоугольная диметрия;
– косоугольная диметрия (кавальерная аксонометрия или кабинетная диметрия);
– косоугольная изометрия (военная аксонометрия).
В архитектурном проектировании могут применяться и другие виды аксонометрий, продиктованные композиционными соображениями.

13.1. Прямоугольная изометрия
Для прямоугольной изометрии показатели искажения равны: u=v=w=0,82 (согласно формуле (1)). Углы между аксонометрическими осями равны 1200 (рис.13.3). Приведенные показатели искажения принимаются равными: U=V=W=1. Соответственно по аксонометрическим осям измеряются координаты X/=UX=X, Y/=VY=Y, Z/=WZ=Z. В результате изображение в аксонометрической проекции оказывается увеличенным по сравнению с соответствующим изображением на комплексном чертеже в U/u=1/0,82=1,22. На рис.13.3 показан комплексный чертеж куба и его изометрическое изображение. Окружности, расположенные в плоскостях, параллельных координатным, проецируются в ортогональной изометрии в виде эллипсов, величины и направление осей которых представлены на рис.13.3.

13.2. Прямоугольная диметрия
В прямоугольной диметрии показатели искажения по осям X/ и Z/ равны u=w=0,94, а по оси Y/: v=0,47 (согласно формуле (1)). Углы между осями X/,Y/ и горизонтальной прямой равны 70 и 410 соответственно. На практике эти углы можно откладывать, исходя из построений на рис.13.4. Приведенные показатели искажения равны U=W=1, V=0,5. Соответственно по осям измеряются координаты X/=UX=X, Y/=VY=0,5Y, Z/=WZ=Z. В результате изображение оказывается увеличенным по сравнению с соответствующим комплексным чертежом в U/u=1/0,94=1,06. Окружности, расположенные в плоскостях, параллельных координатным, проецируются в ортогональной диметрии в виде эллипсов, величины и направление осей которых представлены на рис.13.4.

Зарегистрируйтесь для получения полного доступа к видеоконтенту!